|
|
ПаскальСиАссемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации |
Сила АмпераДата добавления: 2014-04-24; просмотров: 2566; Нарушение авторских прав
|
Уроки php mysql Программирование Онлайн система счисления Калькулятор онлайн обычный Инженерный калькулятор онлайн Замена русских букв на английские для вебмастеров Замена русских букв на английские
Аппаратное и программное обеспечение
Графика и компьютерная сфера
Интегрированная геоинформационная система
Интернет
Компьютер
Комплектующие компьютера
Лекции
Методы и средства измерений неэлектрических величин
Обслуживание компьютерных и периферийных устройств
Операционные системы
Параллельное программирование
Проектирование электронных средств
Периферийные устройства
Полезные ресурсы для программистов
Программы для программистов
Статьи для программистов
Cтруктура и организация данных
| |||||||||
|
Не нашли то, что искали? Google вам в помощь! |
© life-prog.ru При использовании материалов прямая ссылка на сайт обязательна. |

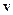 , будет действовать магнитная составляющая силы Лоренца (12.4). Ее часто называют просто силой Лоренца. Выделим элемент проводника с током
, будет действовать магнитная составляющая силы Лоренца (12.4). Ее часто называют просто силой Лоренца. Выделим элемент проводника с током 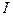 , который характеризуется вектором
, который характеризуется вектором 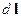 (рис.18.1).
(рис.18.1).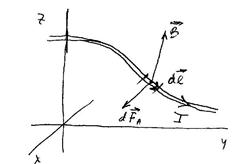
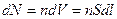 . Сила, действующая на каждый носитель заряда, передается атомам проводника (хотя носители и свободные, но не настолько, чтобы совсем не взаимодействовать с атомами). Результирующая сила, действующая на элемент с током
. Сила, действующая на каждый носитель заряда, передается атомам проводника (хотя носители и свободные, но не настолько, чтобы совсем не взаимодействовать с атомами). Результирующая сила, действующая на элемент с током 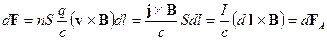 . (18.1)
. (18.1)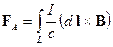 . (18.2)
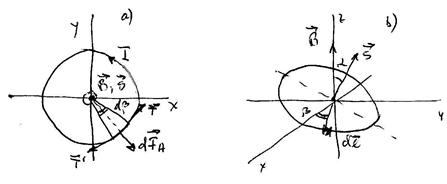
. (18.2)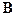 . Если магнитное поле направлено перпендикулярно плоскости витка, пусть для определенности
. Если магнитное поле направлено перпендикулярно плоскости витка, пусть для определенности  (рис.18.2а), то результирующая сила Ампера, как и суммарный момент сил Ампера, будут равны нулю. Положительное направление вектора
(рис.18.2а), то результирующая сила Ампера, как и суммарный момент сил Ампера, будут равны нулю. Положительное направление вектора 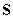 выбираем таким, чтобы, глядя с этого направления, ток в контуре был направлен против часовой стрелки.
выбираем таким, чтобы, глядя с этого направления, ток в контуре был направлен против часовой стрелки.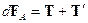 . Проекция этого векторного равенства на направление биссектрисы угла
. Проекция этого векторного равенства на направление биссектрисы угла 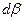 даст нам следующее уравнение:
даст нам следующее уравнение: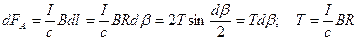 .
.
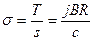 ,
,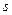 - площадь сечения проводника,
- площадь сечения проводника, 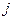 - плотность тока в нем.
- плотность тока в нем.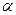 (рис.18.2b). В этом случае результирующая сила Ампера, действующая на контур, будет опять же равна нулю, а момент сил Ампера будет направлен по оси х и его модуль будет равен:
(рис.18.2b). В этом случае результирующая сила Ампера, действующая на контур, будет опять же равна нулю, а момент сил Ампера будет направлен по оси х и его модуль будет равен: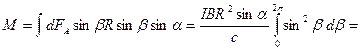
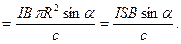
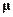 плоского контура с током:
плоского контура с током: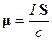 . (18.3)
. (18.3)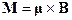 . (18.4)
. (18.4)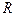 с током
с током 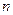 . Магнитное поле вне соленоида пренебрежимо мало, внутри соленоида поле определяется выражением (16.6). Можем считать, что эффективное поле, в котором находится оболочка соленоида с током, равно половине поля в соленоиде:
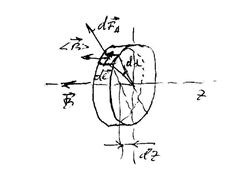
. Магнитное поле вне соленоида пренебрежимо мало, внутри соленоида поле определяется выражением (16.6). Можем считать, что эффективное поле, в котором находится оболочка соленоида с током, равно половине поля в соленоиде: 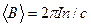 . На рис.18.3 показана часть длинного соленоида толщины
. На рис.18.3 показана часть длинного соленоида толщины  .
.
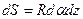 , будет равна:
, будет равна: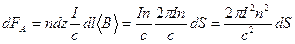 .
. .
.