Для текущей идентификации предпочтительнее рекуррентные процедуры, исключающие необходимость обращения с одной стороны, а с другой позволяют идентифицировать модель в реальном времени по постоянно поступающим эмпирическим данным. В рекуррентном алгоритме МНК присутствует параметр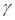 
, который регулирует скорость сходимости или определяет весовые коэффициенты вновь получаемых измерений по отношению к уже имеющимся. Идентификацию можно представить как обычный процесс регулирования, но не выходных величин какого-то объекта, а параметров модели функцией невязки между прогнозом по модели и реальным значением: 
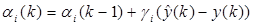, где k – момент или номер измерения, i – номер параметра.
Рис. 9.5.
Если 
взять большим, то ошибки попадут в модель.
Чтобы его получить, достаточно записать выражения для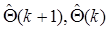 
и второе вычесть из первого. В результате получим
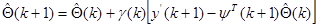(9.19)
(9.20)
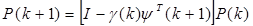(9.21)
Начальные значения принимаются равными
(9.22)
где a должно быть достаточно большим.
Формулу (9.19) можно записать и так:
(9.23)
Заметим, что математическое ожидание матрицы Р с точностью до скалярного множителя равно ковариационной матрице вектора оценок параметров модели
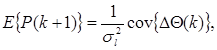
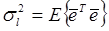(9.24)
