Пусть теперь имеется дискретный объект, описываемый разностным уравнением:
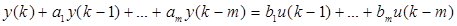(9.6)
Допустим, что нам известны оценки параметров модели объекта 
, полученные после k-1 такта, а также измеренные значения входов и выходов 
. Подставив их в (9.6), определим прогнозируемые (предсказанные) значения выходной переменной. Обозначим его 
:
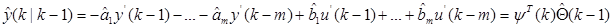
(9.7)
где
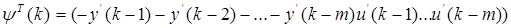(9.8)
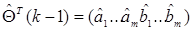(9.9)
После того, как значение y(k) измерено, мы можем вычислить невязку- ошибку прогноза:
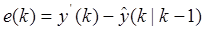(9.10)
Допустим, что измерения выполнены для k=1,2…,m+N. Тогда мы можем записать систему из N+1 уравнения в виде
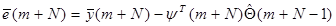(9.11)
где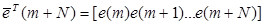 
(9.12)
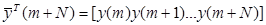(9.13)
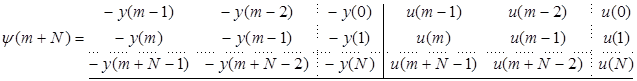
(9.14)
Функцию потерь примем в виде (3), т.е.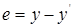 
и получаем
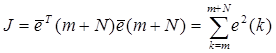(9.15)
Значения оценок параметров 
находятся, как и выше из уравнений
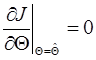. (9.16)
Полагая, что N³2m, обозначим
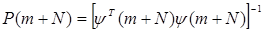. (9.17)
Тогда для вычисления оценок получим общий алгоритм
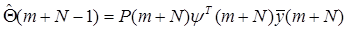(9.18)
Это нерекуррентный алгоритм. В нем необходимо обращать матрицу (9.17). Из (9.14) следует, что её размерность 
, где 2m общее число оцениваемых параметров модели. Обычно m велико и обращение трудоёмко.
