Задача идентификации параметров объекта состоит в следующем. Имеется обучаемая модель объекта
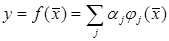, (9.1)
имеется обучающая выборка
(9.2)
Требуется определить модель f так, чтобы прогнозируемые по модели (1) значения у минимально отличались от измеренных значений y’ при одних и тех же значениях входных переменных x’. В качестве меры близости прогнозируемых значений у к измеренным y’ чаще всего используют квадратичную ошибку
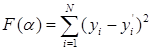(9.3)
Подставив сюда у в соответствии с (9.1), получим
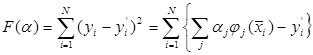(9.4)
Наилучшее приближение соответствует минимальному значению (9.4). В нём все величины, кроме параметров a j, заданы. И только их значениями можно влиять на значение F(a). Известно, что значения a, при которых достигается экстремум, находятся приравниванием нулю производных. Таким образом, получаем систему уравнений
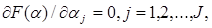(9.5)
где J – количество параметров.
