Решение разностных уравнений состояния

Теорема 1. Рассмотрим разностное уравнение состояния

x(i+1) = A(i) x(i) + B(i) u(i) (7.10)

Решение его может быть представлено в виде

x(i) = Ф(i,i₀)x(i₀) + Ф(i,j+1)B(j)u(j), i³i₀ + 1 (7.11)

где Ф(i,i₀), i ³ i₀ есть матрица

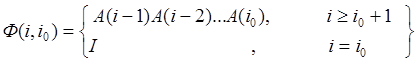(7.12)

Переходная матрица Ф( ) является решением матричного уравнения

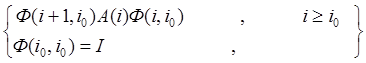(7.13)

Если система стационарная , то

А(i) = A 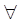i

Ф(i,i₀) = A^{i - i}₀ (7.14)

Формулы (7.11) и (7.12) могут быть получены непосредственно по модели (7.10), если в ней выражать х(i) через x(i-1), x(i-1) - через x(i-2) и так далее до x(i₀).

Выходная переменная описывается уравнением (7.9), пусть x(i₀) = 0. Подставив (7.11) в (7.9) получим следующую зависимость для выходной переменной y(i):

y(i) = 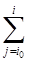K(i,j) u(j), i ³ i₀ , (7.15)

где

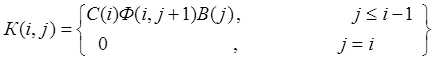(7.16)

(7.16) представляет собой матричную импульсную переходную функцию системы. Если А постоянная матрица, то К(i,j) = К(i-j). Если система имеет прямую связь, т.е. если выходная переменная описывается следующим образом:

y(i) = C(i)x(i) + D(i)u(i) (7.17),

то

(7.18)