Во многих ситуациях целесообразно перейти от непрерывной модели к дискретной. Для преобразования сигналов существуют преобразователи (например, непрерывных в дискретные импульсный элемент и фиксатор нулевого порядка для обратного преобразования).
Преобразование непрерывной модели объекта в дискретную может осуществляться приближенно, опираясь на замену дифференциалов в уравнениях отношениями конечных разностей, или более точно следующим образом. Пусть имеется объект, описываемый дифференциальными уравнениями
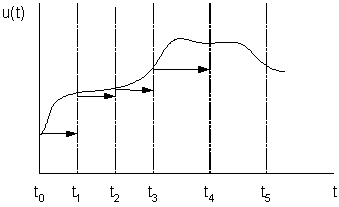
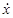(t) = A(t)x(t) + B(t)u(t) (7.5)
y(t) = C(t)x(t) (7.6)
u(t) = u(ti) "tÎ[ti ,ti+1)
Уравнение (7.5) есть уравнение (5.1) и его решение имеет вид (5.9):
x(t) = Ф (t,t0)x(t0) +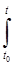 
Ф (t,t) B(t) u(t)dt (7.7)
обозначим t = ti+1 « i+1, t0 = ti « i, u(t) = u(t0) " t0 £ t < t;
А(i ) = Ф(i+1,i) = Ф(t, t0), В(i ) =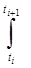
Ф(ti+1 ,t ) В(t)dt .
Применив эти обозначения, получим из (7.7)
x(i+1) = A(i)x(i) + B(i)u(i) (7.8)
y(i+1) = C(i+1) x(i+1) (7.9)
Если система стационарная, то матрицы вычисляются особенно просто
Ф(t,t0) = eA(t-t0) =eADt, òФ(t,t) dt B= ò e A(t - t) B
