Должно быть li < 0 – действительные части.
Пусть а0 > 0
а0р + а1 = 0.
l = -a1/ a0,
Если a1 > 0, то l<.
a0 (p -l1 )(p - l2 ) ... (p -ln ) = 0 раскрыв при условии li > или li,i+1=a+jb и a > мы получим хотя бы один отрицательный коэффициент. Отсюда можно сформулировать необходимое условие устойчивости: необходимым условием устойчивости является положительность всех коэффициентов системы.
Достаточное требует дополнительных условий. Они сформулированы Раусом и Гурвицем в виде критерия Гурвица: для устойчивости необходимо и достаточно чтобы все определители Гурвица были больше нуля.
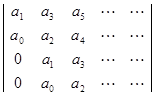 >0
>0
Алгоритм Рауса позволяет проверить устойчивость более просто.
Пусть а0 , а1 . ............,аn коэффициенты характеристического уравнения, тогда
от j = 1 до n -1
1) вычислить значение rj=an-j+1/ an-j (*)
если rj £ , то многочлен неустойчив, иначе 2)
2) от k = 1 определить значение a n-2k - j + 1 = a n-2k - j + 1 - rj a n-2k - j (**)
вернуться к 1).
Если все rj , j = 1, 2, ..., n-1 больше 0, то многочлен устойчив.