Уравнение апериодического звена второго порядка
T1T2y''(t) + (T1 + T2)y′(t) + y(t) = kx(t). (8.15)
Передаточная функция звена равна
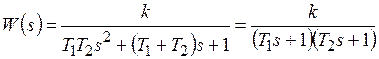. (8.16)
Апериодическое звено второго порядка можно представить в виде последовательного соединения двух звеньев первого порядка с постоянными времени Т1и T2, поэтому оно не относится к числу элементарных. Корни характеристического уравнения действительные.
Частотные характеристики изображены на рис. 8.6:
АФХ: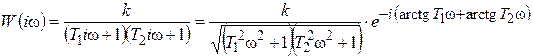 
;(8.17)
АЧХ: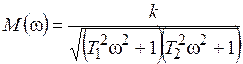 
; (8.18)
ФЧХ: j(w)= –(arctgT1w + arctgT2w). (8.19)
Пунктиром показаны частотные характеристики апериодического звена первого порядка. При сравнении частотных характеристик видно, что добавление второго апериодического звена первого порядка увеличивает инерционность объекта.
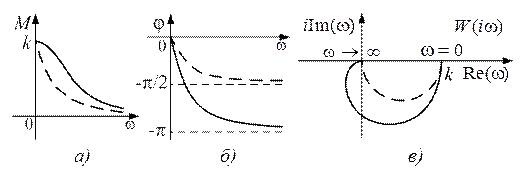
Рис. 8.6. Частотные характеристики апериодического звена второго порядка:
а) АЧХ; б) ФЧХ; в) АФХ
Переходные характеристики изображены на рис. 8.7.
Переходная функция
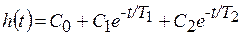, (8.20)
где 
,
представляет собой неколебательную кривую, имеющую одну точку перегиба и асимптотически стремящуюся к y(∞) = k. Весовая функция
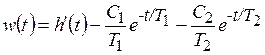. (8.21)
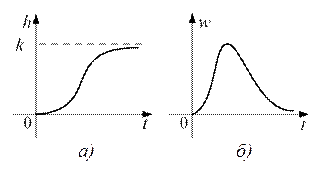
Рис. 8.7 Переходные характеристики апериодического звена второго порядка:
а) переходная функция; б) весовая функция
