Инерционно-форсирующее звено называют также интегро-дифферен-цирующим или упругим звеном
Ty(t) + y(t) = k[T0x'(t) + x(t)]. (8.8)
Существенным параметром звена является коэффициент t = T0/T. Если τ < 1, то звено по своим свойствам приближается к интегрирующему и инерционному звеньям, если же τ > 1, то звено ближе к дифференцирующим звеньям. Передаточная функция звена
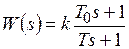(8.9)
Частотные характеристики приведены на рис. 8.3 и 8.4:
АФХ: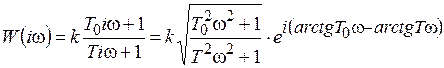 
; (8.10)
АЧХ: 
; (8.11)
ФЧХ: j(w) = arctgT0w – arctgTw. (8.12)
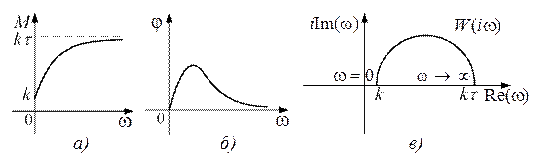
Рис. 8.3. Частотные характеристики инерционно-форсирующего звена для τ > 1:
а) АЧХ; б) ФЧХ; в) АФХ
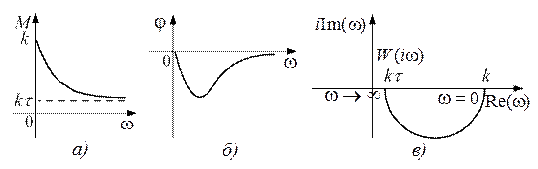
Рис.8.4 Частотные характеристики инерционно-форсирующего звена для τ < 1:
а) АЧХ; б) ФЧХ; в) АФХ
Уравнения переходной и весовой функций, соответственно
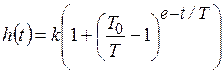, (8.13)
, (8.14)
их графики для τ > 1 и τ < 1 изображены на рис. 8.5.
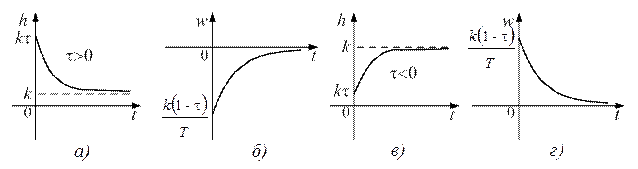
Рис. 8.5. Переходные характеристики инерционно-форсирующего звена
для τ > 1: а) переходная функция, б) весовая функция;
для τ < 1: в) переходная функция, г) весовая функция
