Апериодическое звено первого порядка называется также инерционным. Оно описывается дифференциальным уравнением первого порядка
Ty(t) + y(t) = kx(t). (8.1)
Постоянная времени характеризует инерционность звена.
Передаточная функция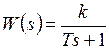 
. (8.2)
Частотные характеристики представлены на рис. 8.1:
АФХ: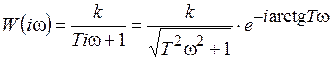 
; (8.3)
АЧХ: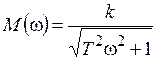 
; (8.4)
ФЧХ: j(w) = –arctgTw. (8.5)
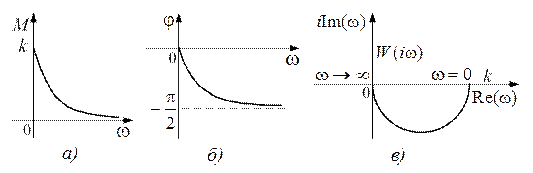
Рис. 8.1. Частотные характеристики апериодического звена первого порядка:
а) АЧХ; б) ФЧХ; в) АФХ
АЧХ апериодического звена первого порядка на нулевой частоте равна коэффициенту усиления k, с увеличением частоты она монотонно уменьшается, асимптотически стремясь к нулю. Фазочастотная характеристика при увеличении частоты от 0 до ∞ изменяется от 0 до –p/2. Следовательно, годограф АФХ для ω > 0 целиком лежит в четвертом квадранте и представляет собой полуокружность диаметром k с центром в точке k/2.
Временные характеристики изображены на рис. 8.2.
Рис. 8.2 Переходные характеристики апериодического звена первого порядка:
а) переходная функция; б) весовая функция
Переходная функция h(t) = k[1 – e–t/T]. (8.6)
Весовая функция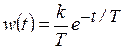 
. (8.7)
