Уравнение звена чистого запаздывания y(t) = x(t – τ). (7.36)
Передаточная функция: W(s) = e–sτ. (7.37)
Графики частотных характеристик изображены на рис. 7.10:
АФХ: W(iw) = e–iwτ; (7.38)
АЧХ: M(ω) = 1; (7.39)
ФЧХ: j(ω) = –wt. (7.40)

Риc. 7.10. Частотные характеристики звена чистого запаздывания:
а) АЧХ; б) ФЧХ; в) АФХ
Так как М(ω) = 1, а отставание по фазе выходных колебаний прямо пропорционально частоте с коэффициентом пропорциональности равным времени чистого запаздывания, то годограф АФХ представляет собой окружность единичного радиуса с центром в начале координат.
Переходные характеристики:
переходная функция: h(t) = 1(t – τ); (7.41)
весовая функция: w(t) = (t – τ). (7.42)
Графики переходных характеристик изображены на рис. 7.11.
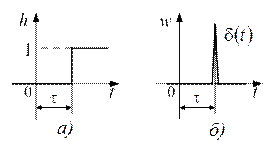
Рис. 7.11. Переходные характеристики звена чистого запаздывания:
а) переходная функция; б) весовая функция