Идеальных дифференцирующих звеньев в природе не существует. Объект, обладающий дифференцирующими свойствами, описывается как реальное дифференцирующее звено
Ty¢(t) + y(t) = Tдx¢(t). (7.22)
Передаточная функция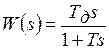 
. (7.23)
Частотные характеристики представлены на рис. 7.6:
АФХ: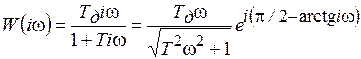 
; (7.24)
АЧХ: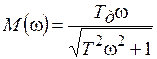 
; (7.25)
ФЧХ: j = p/2 – arctgTw. (7.26)
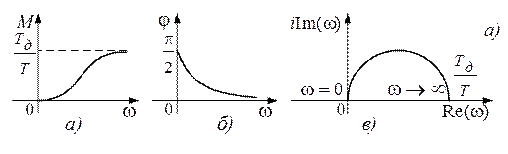
Рис. 7.6. Частотные характеристики реального дифференцирующего звена:
а) АЧХ; б) ФЧХ; в) АФХ
У реального дифференцирующего звена верхний предел амплитудно-частотной характеристики ограничен величиной Тд/Т. Фазочастотная характеристика при увеличении частоты уменьшается от π/2 до нуля. АФХ представляет собой полуокружность диаметром Тд/Т.
Переходная функция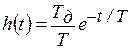 
; (7.27)
весовая функция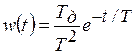 
. (7.28)
На рис. 7.7показаны переходные характеристики реального дифференцирующего звена.
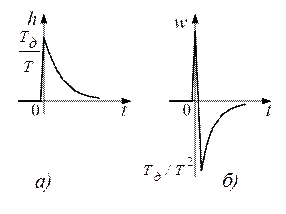
Рис. 7.7. Переходные характеристики реального дифференцирующего звена:
а) переходная функция; б) весовая функция
В силу инерции реальных звеньев изменение переходных характеристик происходит постепенно. Для того, чтобы приблизить свойства реального звена к свойствам идеального, необходимо одновременно увеличивать коэффициенты передачи Тд и уменьшать постоянную времени Т так, чтобы их произведение ТдТ оставалось постоянным.
