Уравнение идеального дифференцирующего звена
y(t) = kx¢(t), (7.15)
то есть изменение выходной координаты пропорционально скорости изменения входной координаты.
Передаточная функция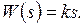 
(7.16)
Частотные характеристики изображены на рис. 7.4:
АФХ: W(iw) = k×iw = kweip/2; (7.17)
АЧХ: M(w) = kw; (7.18)
ФЧХ: j(w) = p/2. (7.19)
Рис. 7.4. Частотные характеристики идеального дифференцирующего звена:
а) АЧХ; б) ФЧХ; в) АФХ
АЧХ прямо пропорциональна частоте, а ФЧХ не зависит от частоты и равна π/2. Годограф АФХ совпадает с положительной ветвью мнимой оси. Переходная функция идеального дифференцирующего звена имеет вид:
h(t) = k×1¢(t) = kd(t), (7.20)
то есть представляет собой δ-функцию с площадью, равной k.
Весовая функция представляет собой производную от δ-функция
w(t) = kd¢(t). (7.21)
Временные характеристики изображены на рис. 7.5.
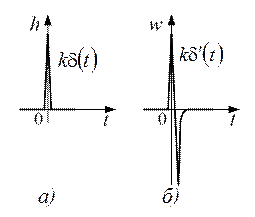
Рис. 7.5. Переходные характеристики идеального дифференцирующего звена:
а) переходная функция; б) весовая функция
