Уравнение движения интегрирующего звена имеет вид
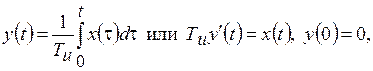(7.8)
где Ти – постоянная времени звена.
Выходной сигнал интегрирующего звена равен интегралу по времени от входного сигнала, умноженному на коэффициент 1/Ти.
Передаточная функция интегрирующего звена:
. (7.9)
АЧХ интегрирующего звена является гиперболической функцией частоты, ФЧХ не зависит от частоты и равна –p/2. АФХ является мнимой функцией частоты, и ее годограф для положительных частот совпадает с отрицательной ветвью мнимой оси.
Графики частотных характеристик изображены на рис. 7.2:
АФХ: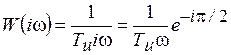 
; (7.10)
АЧХ: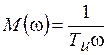 
; (7.11)
ФЧХ: j(ω) = – p/2. (7.12)
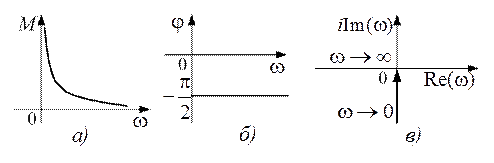
Рис. 7.2. Частотные характеристики интегрирующего звена: а) АЧХ; б) ФЧХ; в) АФХ
Переходные характеристики изображены на рис. 7.3:
переходная функция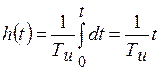 
; (7.13)
весовая функция 
. (7.14)
Рис. 7.3. Переходные характеристики интегрирующего звена:
а) переходная функция; б) весовая функция
Переходная функция интегрирующего звена не имеет установившегося конечного значения. Реакция на δ-функцию является ступенчатой функцией с амплитудой 1/Ти.
