Аппроксимация функций.

Лекция 4

На практике часто неизвестна явная связь между и 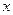, т. е. невозможно записать эту связь в виде некоторой зависимости 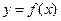.Или запись громоздка, содержит трудно вычисляемые выражения.

Практически важен случай, когда вид связь задается таблицей 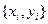. Это означает, что дискретному мно­жеству значений аргумента 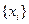поставлено в соответствие множество значений функции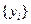 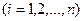. Эти значения — либо результаты расчетов, либо экспериментальные данные. На практике нам могут пона­добиться значения величины и в других точках, отличных от узлов 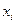. Мы при­ходим к необходимости использования имеющихся табличных данных для приближенного вычисления при любом значении (из некоторой области) параметра 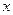, поскольку точная связь 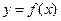не известна.

Задача о приближении (аппроксимации) функций: данную функцию 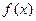требуется приближенно заменить (аппроксими­ровать) некоторой функцией 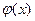так, чтобы отклонение 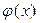от 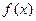в заданной области было наименьшим. Функ­ция 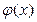при этом называется аппроксимирующей.

Важен случай аппроксимации функции много­членом

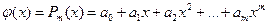(1).

При этом коэффициенты будут подбираться так, чтобы достичь наи­меньшего отклонения многочлена от данной функции.

Если приближение строится на заданном дискретном множестве точек 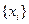, то аппроксимация называется точечной. К ней относятся интерполирование, среднеквадратичное приближение и другие. При построении приближения на непрерывном множестве точек аппроксимация называется непрерывной(или интегральной).