Теорема 1 Если функции 
и 
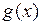дифференцируемы в точке 
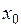, то в этой точке дифференцируемы функции
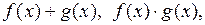
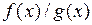(если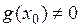 
),
причем 1)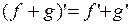 
,
2)
,
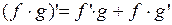3) 
, 
.
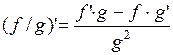Доказательство. 1) Если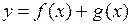 
, то
.
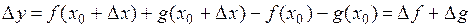Тогда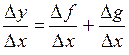 
. При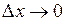 
предел правой части существует, значит, существует и предел левой части. При 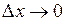получаем .
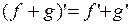2) Пусть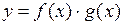 
. Тогда
.
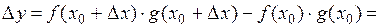
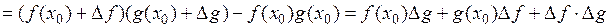Отсюда следует, что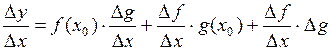 
.
Так как 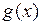дифференцируема в точке 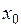, то 
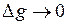при 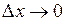. Поэтому из последнего равенства при 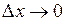получаем
.
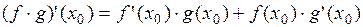3) Доказательство предлагается изучить самостоятельно.■
Следствие 
, где 
.
Пример Доказать, что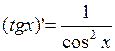 
.
Решение.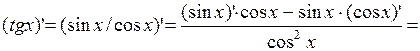 
.
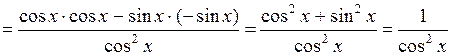Теорема 2 (производная обратной функции) Если функция 
непрерывна и строго возрастает (убывает) на отрезке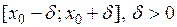 
и если 
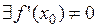, то функция 
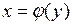, обратная к функции , дифференцируема в точке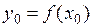 
, причем 
.
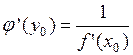Доказательство следует из равенства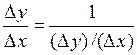 
.
Пример Доказать, что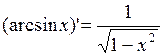 
, при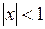 
.
Решение. Здесь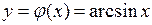 
.
Тогда обратная функция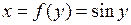 
, 
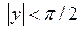. По формуле,
.
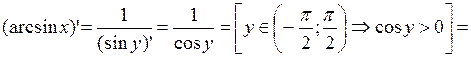
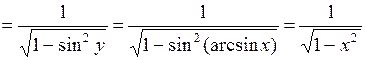Теорема 3 (дифференцирование сложной функции) Если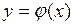 
дифференцируема в точке , 
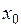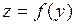дифференцируема в точке 
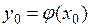, то сложная функция 
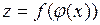дифференцируема в точке 
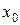, причем 
.
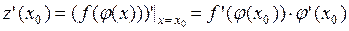