Пусть функции  определена в некоторой окрестности точки
определена в некоторой окрестности точки 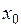 .
.
О. Функция  называется дифференцируемой в точке
называется дифференцируемой в точке 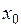 , если её приращение в точке
, если её приращение в точке 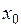 представимо в виде:
представимо в виде:
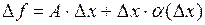 ,
,
где А – постоянная, не зависящая от 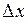 (но зависящая от
(но зависящая от 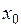 ), а функция
), а функция 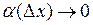 при
при 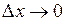 .
.
Слагаемое 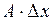 называется дифференциалом функции
называется дифференциалом функции  в точке
в точке 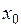 и обозначается
и обозначается 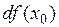 или
или 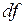 . Дифференциал – это главное линейная часть приращения функции. Тогда
. Дифференциал – это главное линейная часть приращения функции. Тогда  ,
, 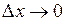 .
.
Теорема Функция  дифференцируема в точке
дифференцируема в точке 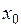 тогда, и только тогда, когда она имеет производную в точке
тогда, и только тогда, когда она имеет производную в точке 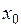 . При этом
. При этом
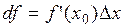 .
.
Доказательство.
Необходимость. Если  дифференцируема в точке
дифференцируема в точке 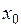 , то приращение функции в точке
, то приращение функции в точке 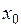 представимо в виде:
представимо в виде:
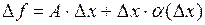 .
.
Отсюда 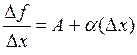 , где
, где 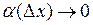 при
при 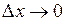 .
.
Следовательно, при 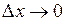 существует
существует 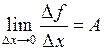 и
и 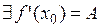 .
.
Достаточность. Если 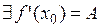 , то
, то 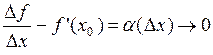 .
.
Следовательно, 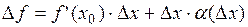 .■
.■
Обычно 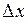 обозначают
обозначают 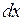 и пишут
и пишут 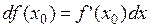 .
.
Механический смысл дифференциала:  , т.е. дифференциал равен расстоянию, которое прошла бы материальная точка за промежуток времени
, т.е. дифференциал равен расстоянию, которое прошла бы материальная точка за промежуток времени 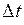 , если бы она двигалась со скоростью
, если бы она двигалась со скоростью 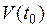 .
.