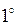 Если
Если  непрерывна в точке а, то она ограничена в некоторой окрестности точки а, т. е.
непрерывна в точке а, то она ограничена в некоторой окрестности точки а, т. е. 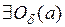 и
и 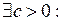
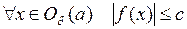 .
.
 Если
Если  непрерывна в точке а, причем
непрерывна в точке а, причем 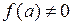 , то существует такая окрестность точки а, в которой знак функции
, то существует такая окрестность точки а, в которой знак функции  совпадает со знаком числа
совпадает со знаком числа 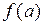 .
.
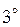 Если
Если  и
и 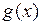 непрерывны в точке а, то функции
непрерывны в точке а, то функции 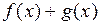 ,
, 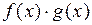 ,
, 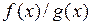 (при условии, что
(при условии, что 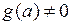 ) непрерывны в точке а.
) непрерывны в точке а.
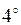 Теорема (непрерывность сложной функции) Если функция
Теорема (непрерывность сложной функции) Если функция  непрерывна в точке
непрерывна в точке 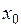 , функция
, функция 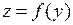 непрерывна в точке
непрерывна в точке 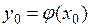 , то в некоторой окрестности точки
, то в некоторой окрестности точки 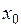 определена сложная функция
определена сложная функция 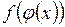 , которая непрерывна в точке
, которая непрерывна в точке 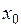 .
.
Доказательство. Возьмем 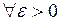 . Так как f непрерывна в точке
. Так как f непрерывна в точке 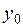 , то
, то 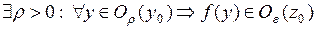 .
.
Так как 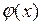 непрерывна в точке
непрерывна в точке 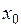 , то для найденной окрестности
, то для найденной окрестности 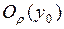
 .
.
Значит, существует окрестность  , на которой определена сложная функция
, на которой определена сложная функция 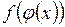 и
и 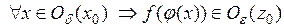 , где
, где
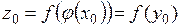 .
.
Итак, 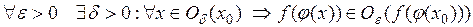 .■
.■