Определение
О. Функция  называется непрерывной в точке а, если она определена в некоторой окрестности этой точки и
называется непрерывной в точке а, если она определена в некоторой окрестности этой точки и 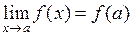 .
.
То есть  непрерывна в точке а, если: 1)
непрерывна в точке а, если: 1)  определена в некоторой
определена в некоторой 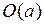 ; 2)
; 2) 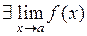 ; 3)
; 3) 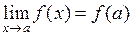 .
.
На языке 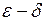 это определение можно записать в виде:
это определение можно записать в виде:
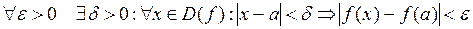 или
или
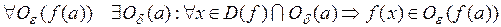 .
.
О. Функция  называется непрерывной слева в точке а, если она определена на
называется непрерывной слева в точке а, если она определена на 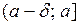 и
и 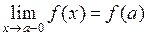 .
.
О. Функция  называется непрерывной справа в точке а, если она определена на
называется непрерывной справа в точке а, если она определена на 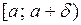 и
и 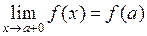 .
.
Примеры 1) 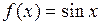 непрерывна
непрерывна 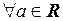 . Действительно,
. Действительно, 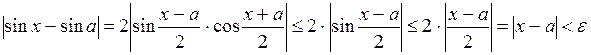 , если взять
, если взять  . То есть
. То есть
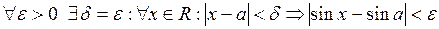 .
.
Следовательно, 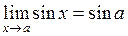 .
.
2) 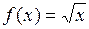 непрерывна
непрерывна 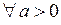 и непрерывна справа в точке
и непрерывна справа в точке 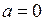 . Действительно,
. Действительно,
при 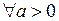
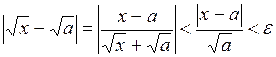 , если
, если 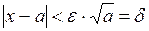 .
.
При 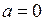
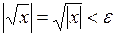 , если
, если 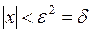 .
.
Итак, 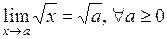 .
.
О. Точка а называется точкой разрыва функции  , если в этой точке функция
, если в этой точке функция  не является непрерывной.
не является непрерывной.
Т.е. а − точка разрыва функции  , если выполняется одно из условий: 1)
, если выполняется одно из условий: 1)  не определена в точке а; 2) не существует
не определена в точке а; 2) не существует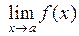 ;
;
3) 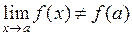 .
.
О. Пусть точка а − точка разрыва функции  . Если в этой точке существуют конечные пределы слева и справа, но они не равны, то точка а называется точкой разрыва I рода функции
. Если в этой точке существуют конечные пределы слева и справа, но они не равны, то точка а называется точкой разрыва I рода функции  .
.
О. Если 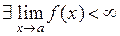 , то точка а называется устранимой точкой разрыва функции
, то точка а называется устранимой точкой разрыва функции  .
.
О. Если в точке а хотя бы один из односторонних пределов не существует или бесконечен, то точка а – точка разрыва II рода функции  .
.
Примеры 1) 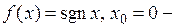 точка разрыва I рода;
точка разрыва I рода;
2)  –устранимая точка разрыва, т.к.
–устранимая точка разрыва, т.к. 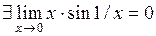 , по теореме о произведении б.м. функции на ограниченную;
, по теореме о произведении б.м. функции на ограниченную;
3) 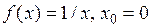 – точка разрыва II рода, т.к.
– точка разрыва II рода, т.к. 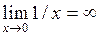 ;
;
4) 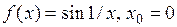 – точка разрыва II рода, т.к.
– точка разрыва II рода, т.к.  не существует.
не существует.