Бесконечно малые функции
Предел монотонной функции
О. Функция называется возрастающей на множестве Х, если
.
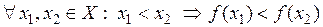О. Функция называется неубывающей на множестве Х, если
.
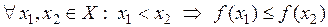О. Функция называется убывающей на множестве Х, если
.
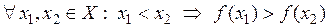О. Функция называется невозрастающей на множестве Х, если
.
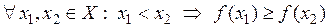Теорема 1 Для того, чтобы неубывающая функция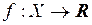 
имела предел при 
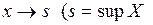или 
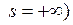, необходимо и достаточно, чтобы функция 
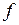была ограничена на Х сверху.
Теорема 2 Для того, чтобы невозрастающая функция 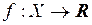имела предел при 
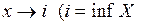или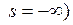 
, необходимо и достаточно, чтобы функция 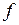была ограничена на Х снизу.
О. Если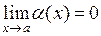 
, то функцию 
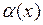называют бесконечно малой при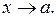 
Свойства бесконечно малых функций
1) Сумма конечного числа б.м. функций при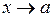 
есть б.м. функция при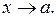
2) Произведение б.м. функции на ограниченную в некоторой проколотой окрестности точки a функцию есть б.м. функция при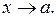
3) Произведение конечного числа б.м. функций при 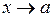есть б.м. функция при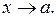
Теорема Есл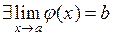и 
и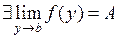 
, причем для любого х из некоторой проколотой окрестности точки a 
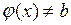, то в точке a существует предел сложной функции 
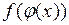и справедливо равенство: 
.
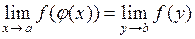