Различные типы пределов
Определение предела по Гейне
О. Число А называется пределом функции  в точке a, если для любой последовательности
в точке a, если для любой последовательности 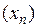 , сходящейся к точке a, и такой, что
, сходящейся к точке a, и такой, что 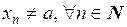 , следует, что последовательность соответствующих значений функции
, следует, что последовательность соответствующих значений функции 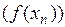 сходится к числу А.
сходится к числу А.
Т.е. 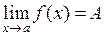
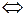
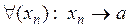 и
и  при
при 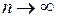 .
.
Пример  не существует.
не существует.
Решение. Для доказательства достаточно указать две последова-тельности, сходящиеся к нулю, такие, что соответствующие значения функции стремятся к различным числам.
Возьмем 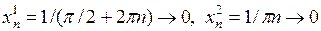 при
при 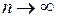 .
.
Но 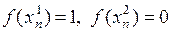 .
.
Теорема Определения предела функции по Коши и по Гейне эквивалентны.
а) Односторонние пределы.
О. Число 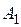 называется пределом слева функции
называется пределом слева функции  в точке a и обозначается
в точке a и обозначается 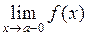 , если
, если
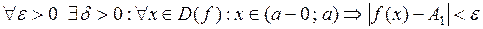 .
.
Аналогично 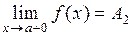 означает, что
означает, что
 .
.
Пределы слева и справа называются односторонними.
Обозначаются также  и
и 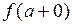 .
.
б) Бесконечные пределы в конечной точке.
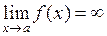 , если
, если 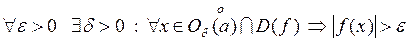 .
.
Например, 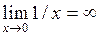 .
.
в) Предел в бесконечности.
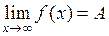 , если
, если 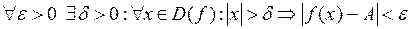 .
.
Например, 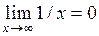 .
.
Свойство1 Если  имеет предел в точке a, то существует такая проколотая окрестность точки a, в которой эта функция ограничена.
имеет предел в точке a, то существует такая проколотая окрестность точки a, в которой эта функция ограничена.
Доказательство. Пусть 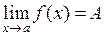 . Тогда для
. Тогда для 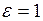
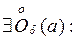
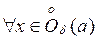
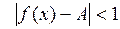 , т. е.
, т. е. 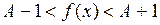 .■
.■
Свойство2 Если 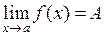 и
и 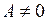 , то существует такая проколотая окрестность точки a, в которой
, то существует такая проколотая окрестность точки a, в которой  имеет тот же знак, что и число А.
имеет тот же знак, что и число А.
Доказательство. Рассмотрим  . Тогда
. Тогда
для 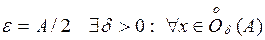
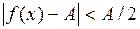 , т. е.
, т. е.
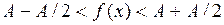 .
.
Значит, 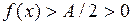 .■
.■
Свойства, связанные с арифметическими операциями
Если  и
и 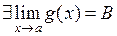 , то
, то
1) 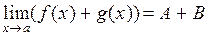 ;
;
2) 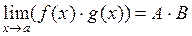 ;
;
3)  , при условии, что
, при условии, что 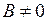 .
.
Частный случай второй формулы: 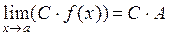 ,
, 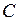 – постоянная.
– постоянная.
Свойства, связанные с неравенствами
1) Если 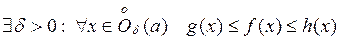 и
и
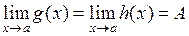 , то
, то 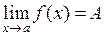 .
.
2) Если 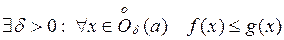 , то
, то 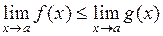 .
.
3) Если 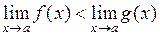 , то
, то 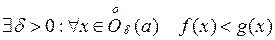 .
.