Предел функции в точке
Критерий Коши сходимости последовательности
O. Последовательность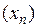 
называется фундаментальной, если
.
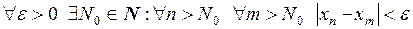Утверждение Если последовательность 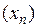фундаментальна, то она ограничена.
Доказательство. Так как 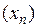фундаментальна, то для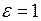 
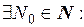
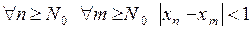. В частности, для 
.
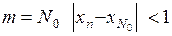Тогда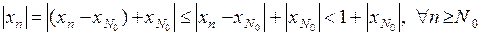 
.
Тогда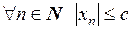 
, где 
.■
Теорема (критерий Коши) Числовая последовательность сходится тогда, и только тогда, когда она является фундаментальной.
Доказательство необходимости. Пусть последовательность 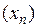сходится. Это значит, что 
.
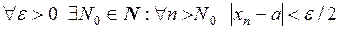Тогда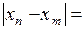 
.
Достаточность предлагается изучить самостоятельно. ■
Пример Покажем, что последовательность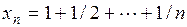 
не является фундаментальной, а значит, в силу критерия Коши, не сходится. Действительно,
.
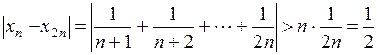То есть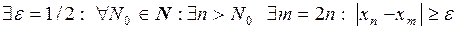 
.
Напомним, что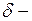 
окрестностью точки a называется множество
.
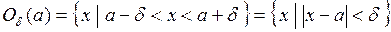Если из этого множества удалить точку a, то получим проколотую окрестность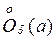 
.
О. Число А называется пределом функции 
в точке a, если
,
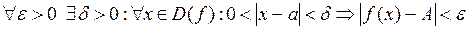то есть для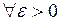 
найдется такое 
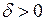, что для 
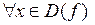, отличающегося от a меньше, чем на 
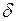, и не равного a, выполняется неравенство 
.
Пишут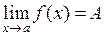 
.
На языке окрестностей 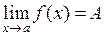означает, что
.
Пример 1 
Решение. Здесь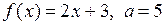 
. Нужно доказать, что
.
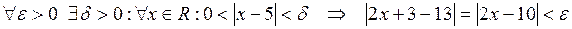Действительно,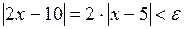 
, если 
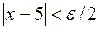. Т. о.,
.
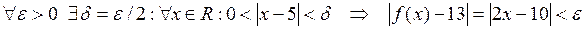Пример 2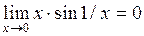 
Решение.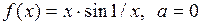 
, 
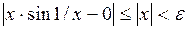, если взять 
.
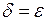Значит,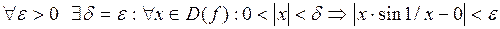 
.
Теорема Если функция имеет предел в точке a, то он − единственный.
Доказательство. Допустим,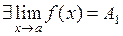 
и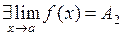 
, причем для определенности будем считать, что 
.
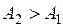Возьмем непересекающиеся окрестности точек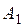 
и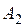 
. Так как 
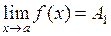, то для 
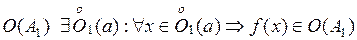. Т. к. 
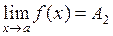, то для 
.
Рассмотрим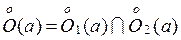 
. Тогда 
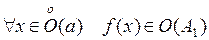и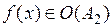 
. Противоречие. ■
