Теорема 1 Если последовательность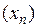 
возрастает и ограничена сверху, то она сходится.
Доказательство. Пусть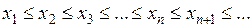 
. Так как 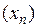ограничена сверху, то множество 
ограничено сверху. Тогда 
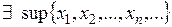. Обозначим 
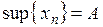. Докажем, что 
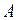– предел .
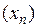Рассмотрим число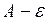 
. Так как 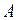является 
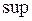, то 
. Т.к. последовательность 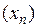возрастает, то 
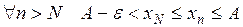. Значит, 
.■
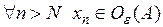Теорема 2 Если последовательность 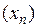убывает и ограничена снизу, то она сходится.
Пример Доказать, что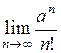 
существует и равен 0 при 
.
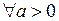Решение. Пусть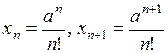 
. Рассмотрим 
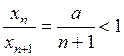, начиная с некоторого номера. Значит, начиная с некоторого номера, 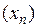убывает. Так как 
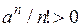, то 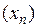ограничена снизу. По теореме 2, 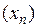сходится. Обозначим 
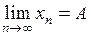. Заметим, что 
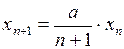. Переходя к пределу в обеих частях последнего равенства при 
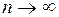, получим 
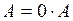. Отсюда 
.
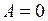Некоторые пределы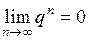 
, при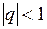 
, 
, 
, 
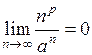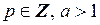
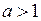
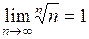
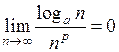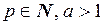
2.9 Число e
Рассмотрим последовательность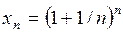 
. Покажем, что она возрастает и ограничена сверху.
Воспользуемся формулой
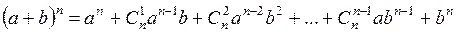, где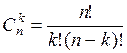 
.
Тогда при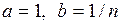 
получим
.
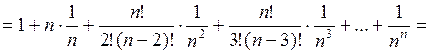
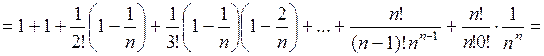
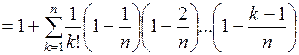Отсюда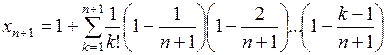 
.
Каждое слагаемое в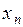 
меньше соответствующего слагаемого в 
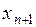, да и слагаемых в 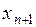больше. Значит, 
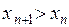. т.е. 
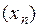возрастает.
Заметим, что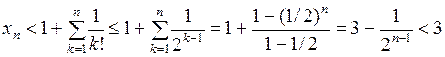 
.
Значит, 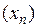ограничена сверху.
По теореме о сходимости монотонной последовательности, 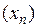имеет предел. Этот предел обозначается буквой e, т.е.
.
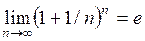