Бесконечно большие последовательности
О. Последовательность называется бесконечно большой, если
 .
.
Пишут 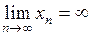 .
.
Пусть 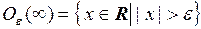 ,
, 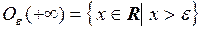 ,
,
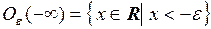 .
.
Тогда 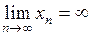
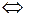
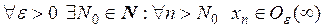 .
.
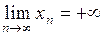
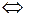
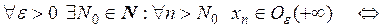
 .
.
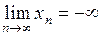
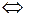
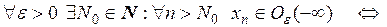
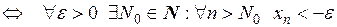 .
.
Утверждение 1) любая бесконечно большая последователь-ность является неограниченной (но не любая неограниченная последовательность является б.б. Например, 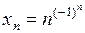 );
);
2) последовательность 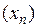 является бесконечно большой тогда, и только тогда, когда последовательность
является бесконечно большой тогда, и только тогда, когда последовательность 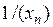 является бесконечно малой.
является бесконечно малой.
Утверждение 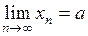
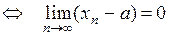 .
.
Доказательство. Оба утверждения равносильны тому, что
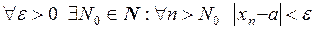 .■
.■
Теорема Если 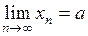 ,
, 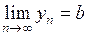 , то
, то
1) 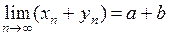 ;
;
2) 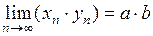 ;
;
3) если 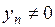 и
и 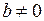 , то
, то 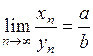 .
.
Доказательство.
1) Так как 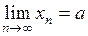 , то
, то
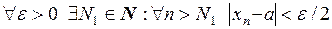 .
.
Так как 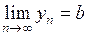 , то
, то 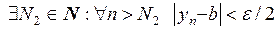 .
.
Тогда 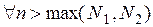
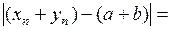
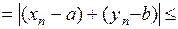
 .
.
2) Надо доказать, что  .
.
Рассмотрим 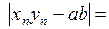
 .
.
Так как 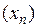 сходится, то она ограничена, т. е.
сходится, то она ограничена, т. е.
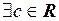 :
: 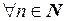
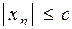 .
.
Если 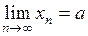 и
и 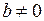 , то
, то
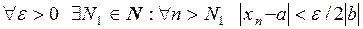 .
.
Так как 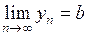 , то
, то 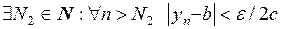 .
.
Тогда  .
.
Если 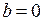 (т.е.
(т.е. 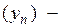 бесконечно малая),
бесконечно малая), 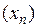 сходится (следовательно, является ограниченной), то
сходится (следовательно, является ограниченной), то 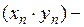 тоже бесконечно малая, и в этом случае утверждение тоже верно.
тоже бесконечно малая, и в этом случае утверждение тоже верно.
3) без доказательства. ■