Свойства сходящихся последовательностей, связанные с неравенствами
Теорема 1 (о промежуточной последовательности или теорема о двух милиционерах) Если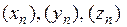 
таковы, что
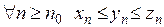и 
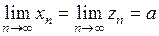, то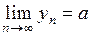 
.
Доказательство. Возьмем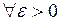 
. Найдем номер 
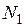так, что 
. Найдем теперь 
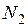так, что 
.
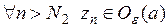Тогда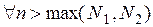 
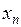и 
.
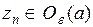Но тогда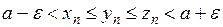 
, т.е. 
.■
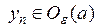Теорема 2 Если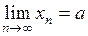 
, 
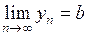, причем 
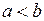, то
.
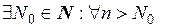
Доказательство. Возьмем непересекающиеся окрестности точек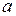 
и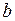 
. Так как 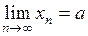, , 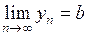то 
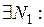
, и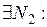 
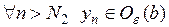. Тогда .■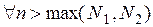
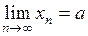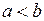Следствие 1 Если и , то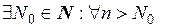 
.
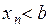Следствие 2 Если 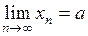, 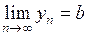и 
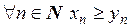, то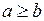 
.
О. Последовательность называется бесконечно малой, если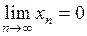 
.
Это означает, что 
.
Свойства бесконечно малых последовательностей:
1) сумма конечного числа б.м. последовательностей есть б.м. последовательность;
2) произведение б.м. последовательности на ограниченную последовательность есть б. м. последовательность.
Доказательство.
1) Пусть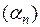 
и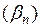 
– б.м. последовательности.
Возьмем 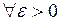. Тогда
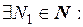
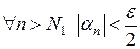и 
.
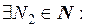
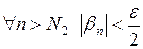Но тогда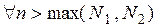 
.
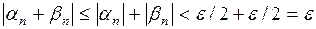Это значит, что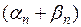 
– бесконечно малая.
2) Пусть 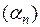– б.м., 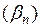– ограниченная последовательность. Тогда
: 
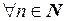
и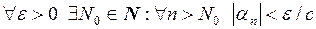 
.
Тогда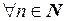 
.■
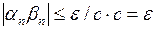