П.4 Интегрирование по частям в определенном интеграле
Теорема Если функции 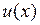 и
и 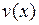 имеют на отрезке
имеют на отрезке  непрерывные производные, то справедлива формула интегрирования по частям:
непрерывные производные, то справедлива формула интегрирования по частям:
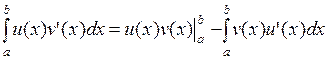 .
.
Для доказательства достаточно проинтегрировать на отрезке 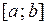 равенство
равенство 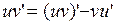 и учесть, что
и учесть, что 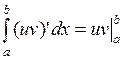 .
.
 §6 Приложения определенного интеграла
§6 Приложения определенного интеграла
О. Криволинейной трапецией называется фигура  , задаваемая на плоскости
, задаваемая на плоскости 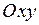 условиями:
условиями: 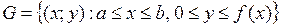 , где
, где  – непрерывная на
– непрерывная на 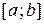 функция.
функция.
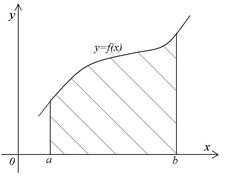
Утверждение Площадь 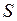 криволинейной трапеции
криволинейной трапеции  вычисляется по формуле:
вычисляется по формуле:
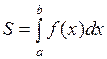 .
.
Доказательство. Пусть  разбиение отрезка
разбиение отрезка  ,
,
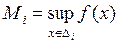 ,
,  ,
,  ,
,  ,
, 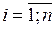 .
.
Рассмотрим фигуру 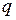 , составленную из прямоугольников
, составленную из прямоугольников  , у которых длина основания равна
, у которых длина основания равна 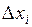 , а высота
, а высота 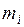 . А также рассмотрим фигуру
. А также рассмотрим фигуру  , составленную из прямоугольников
, составленную из прямоугольников  , длина основания которых равна
, длина основания которых равна 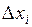 , а высота
, а высота 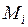 ,
, 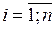 .
.
Очевидно, 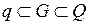 . Площади фигур
. Площади фигур 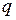 и
и  соответственно равны:
соответственно равны:
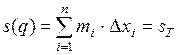 ,
, 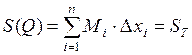 ,
,
где 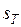 и
и 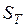 – нижняя и верхняя суммы Дарбу функции
– нижняя и верхняя суммы Дарбу функции  .
.
Значит, 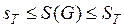 .
.
Так как  непрерывна на
непрерывна на  , то она интегрируема на
, то она интегрируема на  . По критерию интегрируемости
. По критерию интегрируемости  ,
, 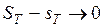 при
при 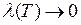 , т.е.
, т.е.
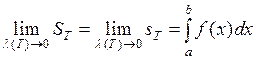 . Значит, и
. Значит, и  ■
■
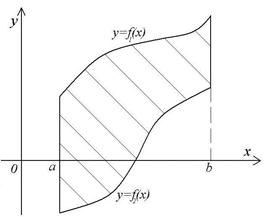
Рассмотрим фигуру  , ограниченную отрезками прямых
, ограниченную отрезками прямых  и графиками непрерывных функций
и графиками непрерывных функций 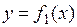 и
и 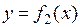 , где
, где 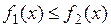 при
при 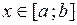 . Если
. Если 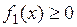 , то площадь фигуры
, то площадь фигуры  равна разности площадей криволинейных трапеций, поэтому
равна разности площадей криволинейных трапеций, поэтому
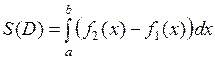 .
.
Последняя формула остается верна и в случае, когда условие 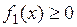 не выполняется.
не выполняется.
Пример Найти площадь фигуры, ограниченной эллипсом 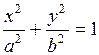 .
.

Решение. Найдем площадь 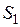 части эллипса, расположенной в первой координатной четверти. Из уравнения эллипса
части эллипса, расположенной в первой координатной четверти. Из уравнения эллипса  ,
,  . Тогда искомая площадь
. Тогда искомая площадь 
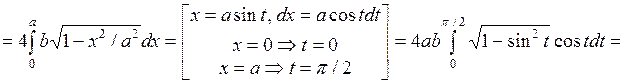

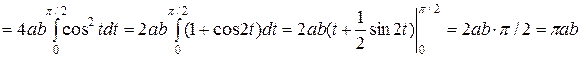 .
.
Аналогично (при 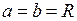 ) можно вычислить площадь круга
) можно вычислить площадь круга 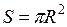 .
.