П.2 Формула Ньютона-Лейбница
Теорема Если функция 
непрерывна на отрезке 
и если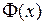 
– какая-нибудь первообразная для функции на этом отрезке, то справедлива формула Ньютона-Лейбница:
.
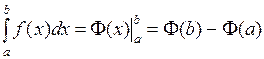Доказательство. Если 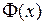– некоторая первообразная для функции , то 
R :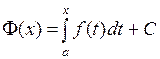 
, 
.
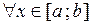Подставим в это равенство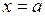 
. Получим 
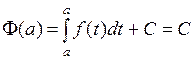. Значит, 
.
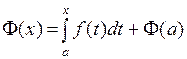Подставим в последнее равенство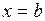 
, получим 
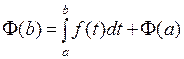. Отсюда 
■
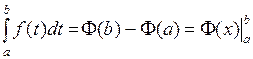Пример 
.
Теорема Пусть непрерывна на отрезке , 
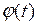имеет непрерывную производную на интервале 
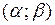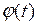, отображает отрезок 
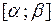на отрезок так, что 
, 
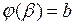. Тогда справедлива формула замены переменной в определенном интеграле:
.
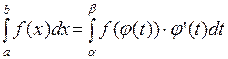Доказательство. Пусть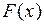 
– первообразная для , тогда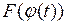 
– первообразная для функции 
.
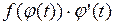По формуле Ньютона-Лейбница, имеем: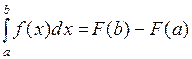 
.
С другой стороны,
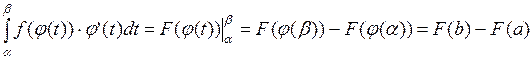
Так как правые части равенств равны, то и левые равны ■
Пример Вычислить интеграл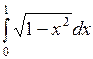 
.
Решение.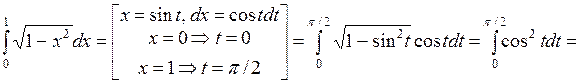
.
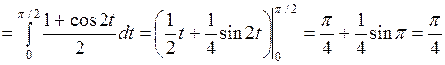Утверждение 1 а) если – нечетная функция, то 
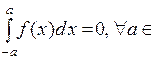R;
б) если – четная функция, то 
R.
Доказательство. а) Так как – нечетная, то 
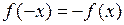. Сделаем замену в интеграле:
.
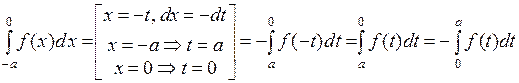Тогда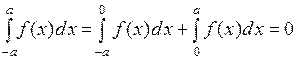 
.
б) Так как – четная, то 
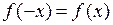. Сделав такую же замену, получим
.
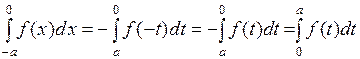Тогда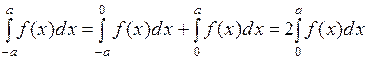 
■
Утверждение 2 Если – периодическая функция с периодом Т, то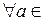 
R имеет место равенство:
.
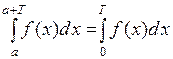Доказательство. По свойствам интеграла,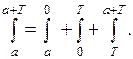 
В последнем интеграле сделаем замену: 
. Если 
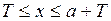, то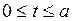 
. Тогда
.
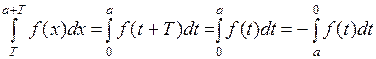Значит,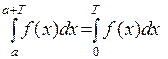 
■
