Теорема Если функция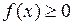 
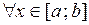и 
интегрируема на отрезке 
, то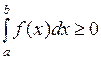 
.
Доказательство следует из того, что при условиях теоремы любая интегральная сумма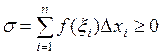 
■
Следствие 1 (о монотонности интеграла) Если функции и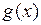 
интегрируемы на отрезке и если 
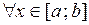
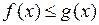, то
.
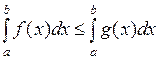Доказательство следует из того, что при условиях теоремы при любом разбиении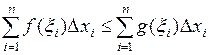 
■
Следствие 2 Пусть функция интегрируема на отрезке и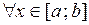 
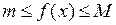. Тогда выполняется неравенство:
.
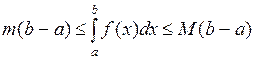Доказательство.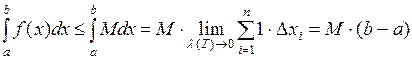 
. Левая часть неравенства доказывается аналогично ■
Теорема Если функция интегрируема на отрезке , то функция 
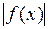тоже интегрируема на и верна оценка:
.
Доказательство. Воспользуемся неравенством:
.
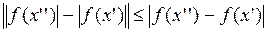Тогда при любом разбиении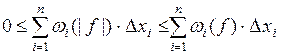 
.
Есл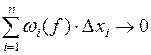и 
при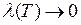 
, то и 
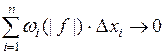. Значит, 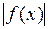интегрируема на .
Рассмотрим неравенство 
.
Перейдем в нем к пределу при 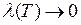. Так как левая часть неравенства стремится к 
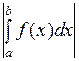, а правая – к 
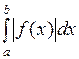, то получим то, что и требовалось доказать ■
