Свойство 1 Если функция 
интегрируема на отрезке 
, то она интегрируема на любом отрезке 
.
Доказательство. Возьмем любое разбиение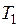 
отрезка 
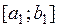. Нужно доказать, что 
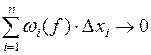при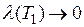 
.
Добавим к 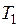точки из 
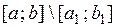так, чтобы 
.
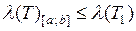Тогда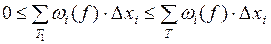 
, так как правая часть содержит все слагаемые левой части.
Устремим 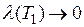, тогда 
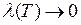, но тогда 
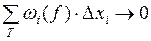, но тогда и 
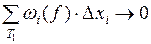. Значит, интегрируема на отрезке ■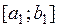
Свойство 2 Если функция интегрируема на отрезке и 
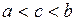, то
.
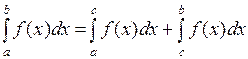Доказательство. Существование интегралов следует из свойства 1. Равенство следует из того, что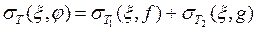 
, где 
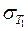и 
– интегральные суммы на отрезках 
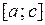и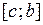 
, причем 
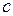является точкой разбиения отрезка .
Если 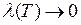, то пределы интегральных сумм 
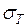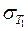, , существуют и выполняется равенство, приведенное в формулировке теоремы ■
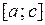Верно и обратное утверждение: если интегрируема на отрезках и 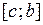, то она интегрируема и на отрезке , и выполняется равенство из свойства 2.
Положим по определению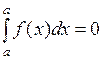 
, 
.
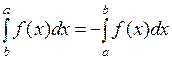Свойство 3 Пусть функция интегрируема на отрезке . Тогда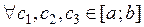 
выполняется равенство:
.
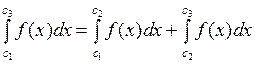Доказательство. Если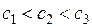 
, то равенство следует из свойства 2. Если 
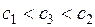, то так как 
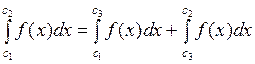, то отсюда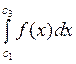 
■
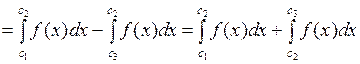