Свойство 1 Если функции  и
и 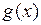 интегрируемы на отрезке
интегрируемы на отрезке  , то
, то 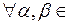 R функция
R функция 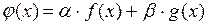 интегрируема на отрезке
интегрируема на отрезке  и выполняется равенство:
и выполняется равенство:
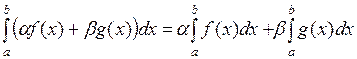 .
.
Доказательство. Составим интегральные суммы для функций  ,
, 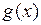 ,
, 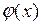 при заданном разбиении отрезка
при заданном разбиении отрезка  и зафиксируем отмеченные точки
и зафиксируем отмеченные точки 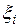 . Тогда имеет место равенство:
. Тогда имеет место равенство:
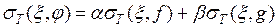 .
.
Перейдем к пределу при 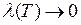 . Так как функции
. Так как функции  и
и 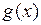 интегрируемы на отрезке
интегрируемы на отрезке  , то правая часть имеет предел, равный
, то правая часть имеет предел, равный 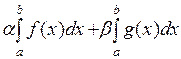 . Тогда и левая часть имеет такой же предел ■
. Тогда и левая часть имеет такой же предел ■
Свойство 2 Если функции  и
и 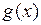 интегрируемы на отрезке
интегрируемы на отрезке  , то функция
, то функция 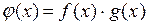 тоже интегрируема на отрезке
тоже интегрируема на отрезке  .
.
Доказательство. Если  и
и 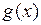 интегрируемы на отрезке
интегрируемы на отрезке  , то они ограничены на нем, т.е.
, то они ограничены на нем, т.е.  R :
R : 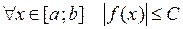 и
и  . Значит,
. Значит, 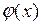 ограничена на
ограничена на  .
.
Рассмотрим 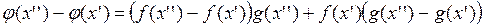 . Тогда
. Тогда 
 .
.
Тогда  .
.
Умножим последнее равенство на 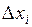 и просуммируем по
и просуммируем по 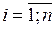 , получим
, получим 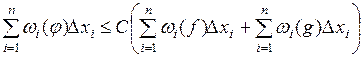 .
.
При 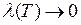 правая часть стремится к нулю, значит, и левая стремится к нулю. Значит,
правая часть стремится к нулю, значит, и левая стремится к нулю. Значит, 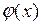 интегрируема на отрезке
интегрируема на отрезке  ■
■