П.5 Классы интегрируемых функций
Теорема 1 Если функция непрерывна на отрезке, то она интегрируема на этом отрезке.
Доказательство. Так как 
непрерывна на отрезке, то (по теореме Кантора) она равномерно непрерывна на нем, т.е.
.
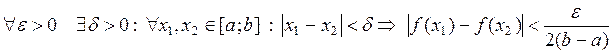Возьмем произвольное разбиение с мелкостью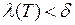 
. Тогда
.
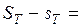
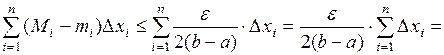
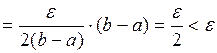Значит, интегрируема на отрезке ■
Теорема 2 Если функция ограничена на отрезке 
и имеет на нем лишь конечное число точек разрыва, то интегрируема на отрезке .
Теорема 3 Если функция определена на отрезке и монотонна на нем, то она интегрируема на этом отрезке.
Доказательство. Пусть, например, функция возрастает на отрезке , тогда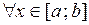 
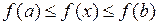. Но отсюда следует, что ограничена на .
Рассмотрим произвольное разбиение Т отрезка .
Так как возрастает, то для 
, 
.
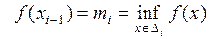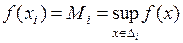Тогда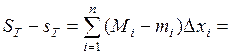 
.
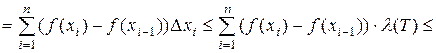
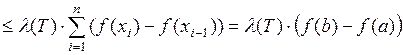Получили, что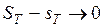 
при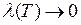 
. А это значит, что интегрируема на отрезке ■
§4 Свойства определенного интеграла
В параграфе 3 был сформулирован критерий интегрируемости функции:
интегрируема на отрезке 
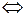
ограничена на и выполняется условие: 
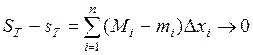при .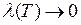
Обозначим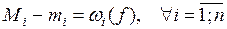 
. Величину 
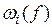называют колебанием функции на отрезке 
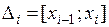. Тогда критерий интегрируемости запишется в виде:
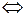
интегрируема на отрезке ограничена на и выполняется условие: 
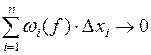при .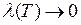
Очевидно, 
.
Далее будем рассматривать только ограниченные функции.
