Пусть функция 
определена на отрезке 
. Разбиением Т отрезка называется множество точек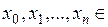 
, таких, что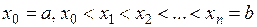 
. Обозначим 
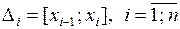– частичный отрезок разбиения, 
– длину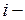 
того отрезка разбиения. 
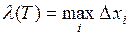назовем мелкостью разбиения Т. Возьмем на каждом отрезке разбиения произвольную точку 
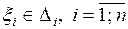. Получим разбиение с отмеченными точками.
Сумма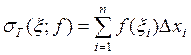 
называется интегральной суммой для функции при заданном разбиении Т и фиксированных отмеченных точках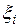 
.
О. Число I называется определенным интегралом от функции по отрезку , если для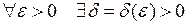 
такое, что для любого разбиения Т, мелкость которого 
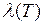меньше 
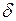, и при любом выборе отмеченных точек 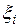выполняется неравенство:
.
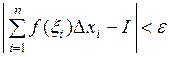Обозначается определенный интеграл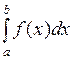 
.
Данное определение интеграла означает, что число I является пределом интегральных сумм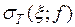 
при мелкости разбиения 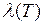, стремящейся к нулю, т.е. 
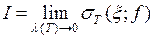, причем предел этот не зависит от выбора отмеченных точек .
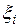Если для функции существует число I, то функцию называют интегрируемой (по Риману) на отрезке , и говорят, что существует интеграл от функции на отрезке .
