Вычисление скалярного произведения векторов через их координаты
Основные свойства скалярного произведения векторов
Определение
Скалярное произведение векторов
· Скалярным произведением геометрических векторов называется число, равное произведению их длин на косинус угла между ними: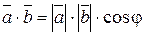 
, где 
.
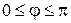Пример 5.Длины векторов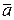 
и 
равны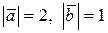 
, а угол между ними 
. Вычислите скалярное произведение 
.
.
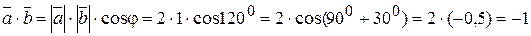1) 
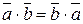(коммутативность);
2) 
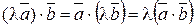(ассоциативность относительно умножения на число);
3) 
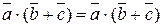(дистрибутивность относительно сложения векторов);
4) 
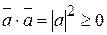- скалярный квадрат равен квадрату модуля вектора и является неотрицательным числом.
Скалярное произведение векторов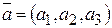 
и 
равно сумме произведений одноименных координат:
.
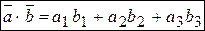Пример 6.Найти скалярное произведение векторов
и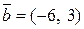 
.
Решение.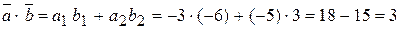 
.
Скалярный квадрат вектора 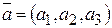равен квадрату его длины 
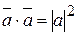, отсюда 
.
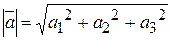Подставив последние формулы в определение скалярного произведения векторов, получим:
.
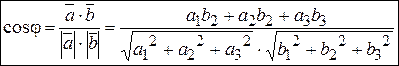Ортогональные векторы – это векторы, угол между которыми равен 900, то есть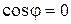 
.
Два ненулевых вектора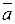 
и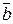 
ортогональны тогда и только тогда, когда их скалярное произведение равно нулю, т.е. сумма произведений одноименных координат равна нулю: 
.
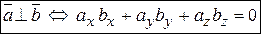Пример 7. Найдите, при каком значении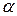 
векторы 
и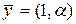 
ортогональны.
Запишем условие ортогональное векторов в координатной форме: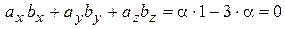 
. Отсюда 
; 
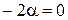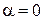. Значит, векторы 
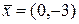и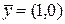 
ортогональны.
