Координаты вектора. Преобразования координат вектора при основных операциях
Дан вектор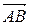 
в пространстве. Известны координаты точек 
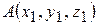и 
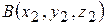. Тогда координаты вектора 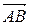вычисляются по правилу: из координат конечной точки нужно вычесть координаты начальной точки: 
.
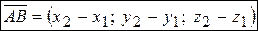При умножении вектора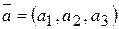 
на число 
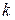его координаты умножаются на это число: 
.
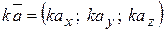При сложении векторов 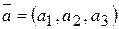и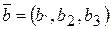 
складываются соответствующие координаты: 
.
Пример 3. На плоскости 
даны точки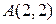 
, 
, 
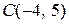. Найдите координаты векторов 
, 
, 
.
;
;
.
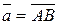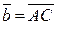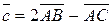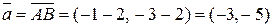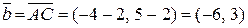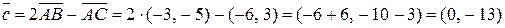Дан вектор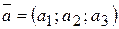 
в пространстве. Модуль вектора 
вычисляется по формуле: 
.
Важной задачей является нахождение расстояния между двумя точками:
1) расстояние между точкам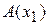и 
и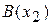 
на прямой равно длине вектора :
;
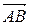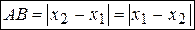2) расстояние между двумя точкам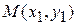и 
и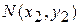 
на плоскости равно длине вектора :
;
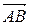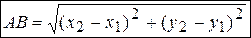3) расстояние между двумя точкам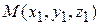и 
и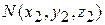 
в пространстве равно длине вектора :
.
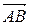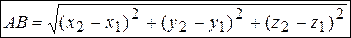Пример 4.Вектор имеет начало в точке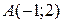 
, а конец - в точке 
. Найдите координаты и длину вектора 
.
Решение
;
.
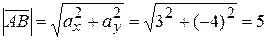