Пусть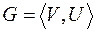 
- некоторый граф. Назовем граф 
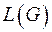реберным графом 
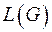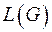, если носитель графа совпадает с множеством ребер графа , и две вершины в смежны, если соответствующие ребра смежны в .
Пример
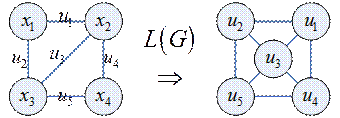(это преобразование можно выполнить всегда)
|
Граф обладает свойством реберности, если существует некоторый граф, реберный для которого является изоморфным для .
Пример
Теорема
Граф обладает свойством реберности, если существует разложение ребер графа на полные подграфы такое, что каждая вершина графа принадлежит не более чем двум полным подграфам.
Замечание
1. Не для любого графа существует такое разложение ребер.
2. В разложении ребер каждое ребро принадлежит ровно одному подграфу.
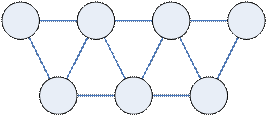
Пример
Пример
| 
|
| не являются реберными
|
Если граф обладает свойством реберности, то как найти его образ (т.е. граф, для которого данный является реберным)?
Пример
:
:
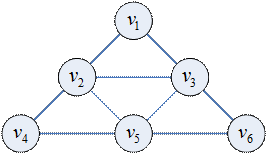
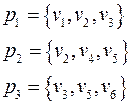
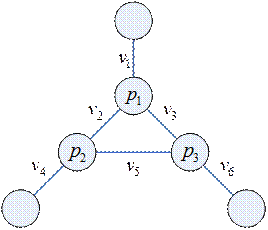
Пример
