Полные подграфы. Плотность графа
Пусть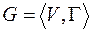 
- некоторый граф. Максимальный по включению вершин подграф графа, любые две вершины которого смежны называется полным подграфом. Мощность максимального полного подграфа называется плотностью графа 
.
Начальный шаг: строится вершина – корень дерева, которой сопоставляется граф 
.
Итерационный шаг: на 
-ом ярусе есть вершина, которой сопоставлен граф 
.
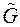а) Из 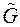выбирается любая вершина 
и выносится на 
ярус.
б) На ярус выносятся все вершины, которые входят в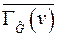 
.
в) Каждая из вершин яруса взвешивается соответствующим графом – окрестностью от графа .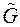
Заключительный шаг: вершина дерева будет висячей, если соответствующий ей граф – пустой граф.
Замечание
В пункте а) желательно выбирать ту вершину, которая имеет максимальную степень.
Задачу нахождения полных подграфов в можно свести к задаче нахождения пустых подграфов в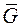 
.
Пример
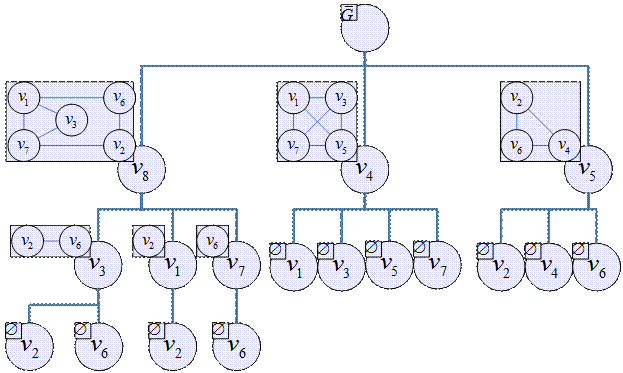
Полные подграфы графа (или пустые подграфы графа ):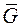
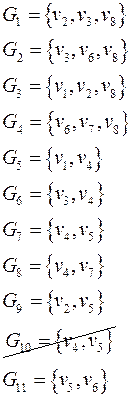
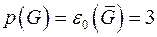
Пример
| :
|
|
Пример
Выделяем пустые подграфы:
