Укладки графа. Планарность
Исследуются топологические свойства графа. Гомеоморфизм графов – еще одно отношение эквивалентности на графах. Два графа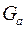 
и 
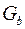гомеоморфны, если они изоморфны с точностью до цепей степени 2.
Пример
: 
| : 
|
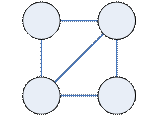
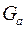| Гомеоморфны. Говорят, что они имеют одну и ту же топологию.
|
Пусть 
- некоторая поверхность. Род поверхности - это максимальное число простых замкнутых кривых, не разделяющих эту поверхность.
| Род плоскости: 0
| 
|
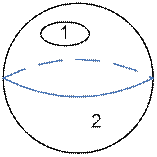
| Род сферы: 0
| 
|
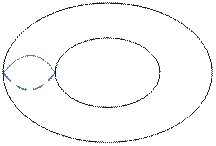
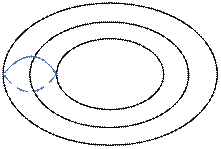
| Род тора: 1
|  
|
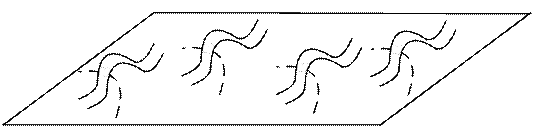
Поверхности, которые имеют род 4:
Род графа 
- 
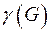- минимальный род поверхности, на которой можно «уложить» граф без взаимных пересечений ребер (ребра пересекаются только в вершинах).
Пример
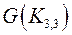
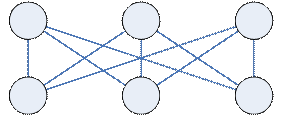
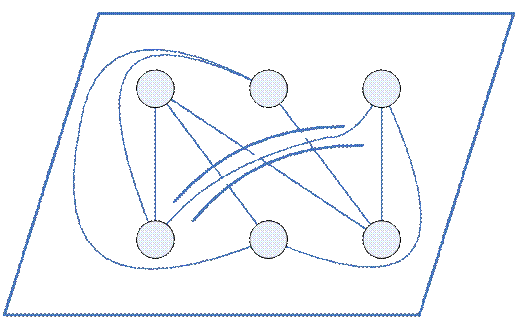
Граф называется планарным(плоским), если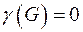 
.
· печатные платы – планарные графы;
· микросхемы (на уровне технологии их изготовления) – планарные графы.
Критерий планарности графа (критерий Понтрягина-Куратовского)
Граф планарен тогда и только тогда, когда в нем отсутствуют подграфы, гомеоморфные 
или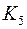 
.
1) Найти все подграф, гомеоморфные и .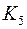
2) Построить таблицу покрытия найденных в п.1 подграфов ребрами, которые их образуют.
3) Найти минимальное покрытие подграфов ребрами (удалив ребра, образующие покрытие, получим планарный граф).
