Внутренняя устойчивость графа
Подмножество вершин графа называется внутренне устойчивым, если они попарно несмежны между собой. Внутренне устойчивое множество вершин называется пустым подграфом, если при добавлении хотя бы одной вершины свойство внутренней устойчивости пропадает.
Пример
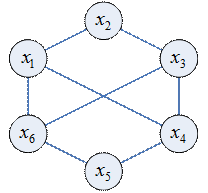
| 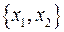 - не является внутренне устойчивым - не является внутренне устойчивым 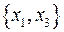 - является внутренне устойчивым (но не является пустым подграфом) - является внутренне устойчивым (но не является пустым подграфом) 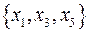 - является внутренне устойчивым (и является пустым подграфом) - является внутренне устойчивым (и является пустым подграфом)
|
Мощность максимального пустого подграфа называется числом внутренней устойчивости графа 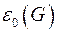 .
.
Пусть 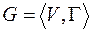 - некоторый граф,
- некоторый граф, 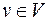 - некоторая вершина,
- некоторая вершина, 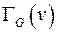 - окрестность вершины
- окрестность вершины  . Неокрестность (коокрестность) вершины
. Неокрестность (коокрестность) вершины  графа
графа  обозначим
обозначим 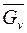 - подграф графа
- подграф графа  , порожденный
, порожденный 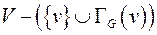 .
.
Теорема
Пустой подграф, содержащий вершину  содержит по крайней мере одну вершину из коокрестности вершины
содержит по крайней мере одну вершину из коокрестности вершины  .
.
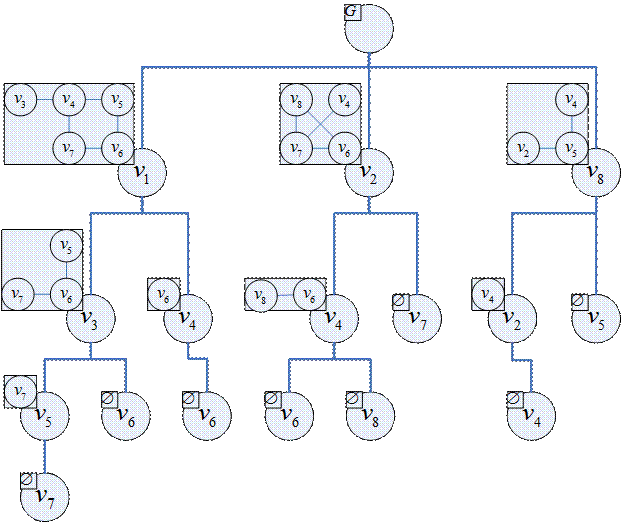
Начальный шаг: строится вершина – корень дерева, которой сопоставляется граф  .
.
Итерационный шаг: на  -ом ярусе есть вершина, которой сопоставлен граф
-ом ярусе есть вершина, которой сопоставлен граф 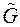 .
.
а) Из 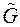 выбирается любая вершина
выбирается любая вершина  и выносится на
и выносится на  ярус.
ярус.
б) На  ярус выносятся все вершины, которые входят в
ярус выносятся все вершины, которые входят в 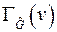 .
.
в) Каждая из вершин  яруса взвешивается соответствующим графом – коокрестностью от графа
яруса взвешивается соответствующим графом – коокрестностью от графа 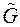 .
.
Заключительный шаг: вершина дерева будет висячей, если соответствующий ей граф – пустой граф.
Замечание
В пункте а) желательно выбирать ту вершину, которая имеет минимальную степень.
Пример