Алгоритм нахождения базисной системы циклов

Цикломатика графа

Пусть 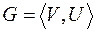- граф. Цикл в графе может быть записан в ви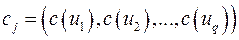де , где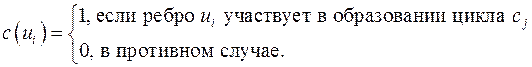

Пример

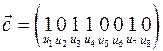
Каждый цикл может быть представлен в качестве двоичного вектора. Множество циклов образует пространство двоичных векторов. Цикломатический базис – совокупность линейно независимых циклов графа, с помощью которых могут быть получены все остальные циклы. Цикломатическое число графа 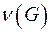- мощность базисной системы циклов графа .

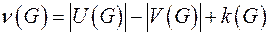
Пример

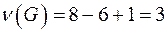
Граф, у которого цикломатическое число равно 0, называется деревом (или ациклическим графом). Многокомпонентный ациклический граф называется деревом. Остов графа – частичный граф исходного графа, в котором число вершин и число компонент связности совпадает с числом вершин и числом компонент связности исходного графа, но цикломатическое число равно 0.

1. Получить остов графа (удалить 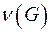ребер; удаляемые ребра называются хордами).
2. Добавляя к остову поочередно по одной хорде получаем базисную систему циклов.

Пример

	остов	хорды

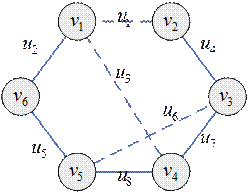
Множество всех циклов графа:

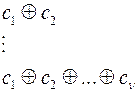
Число циклов в графе не превосходит .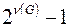

Пример

123

Теорема Кенига
Граф двудолен тогда и только тогда, когда он не содержит циклов нечетной длины.