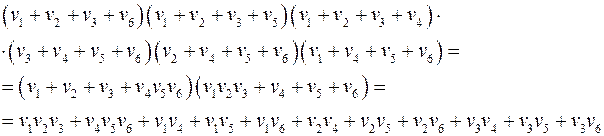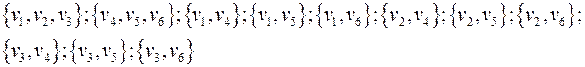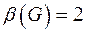Устойчивость графа
Алгоритм нахождения базисной системы разрезов
Разделяющие множества. Разрезы
Пусть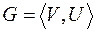 
- некоторый связный граф. Подмножество ребер графа называется разделяющим множеством, если удаление их из графа изменяет число компонент связности. Разделяющее множество называется разрезом графа, если любое его собственно подмножество не является разделяющим.
Пример
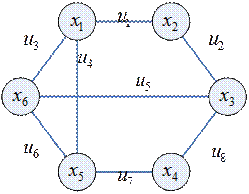
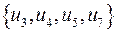- разделяющее множество, разрез.
цикл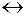 
разрез (коцикл)
Коциклический ранг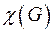 
- число линейно независимых коциклов графа. 
.
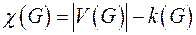Пример
.
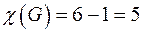1. Построить остов графа 
.
2. Удалять поочередно по одному ребру (остов распадается на две компоненты). Добавить к разрезу те хорды, концы которых принадлежат разным компонентам.
Пример
Число коциклов в графе равно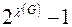 
.
Пусть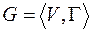 
- некоторый граф. Подмножество вершин 
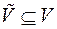называется множеством внешней устойчивости, если
1) 
2) 
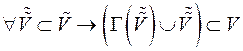
Мощность минимального множества внешней устойчивости называется числом внешней устойчивости графа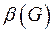 
. Для того, чтобы найти все множества внешней устойчивости графа, надо найти все покрытия модифицированной матрицы смежности графа. Модификация заключается в добавлении единичной главной диагонали.
Пример
Множества внешней устойчивости:
