Циклы в графе
Сети
Нахождение КСС
Теорема
Любая вершина орграфа принадлежит ровно одной КСС орграфа.
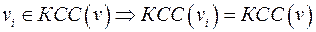
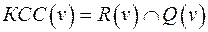, где
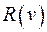- множество вершин, достижимых из 
,
- множество вершин, из которых достижимо .
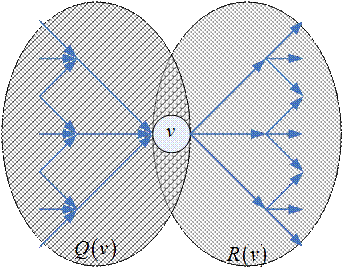
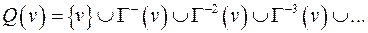
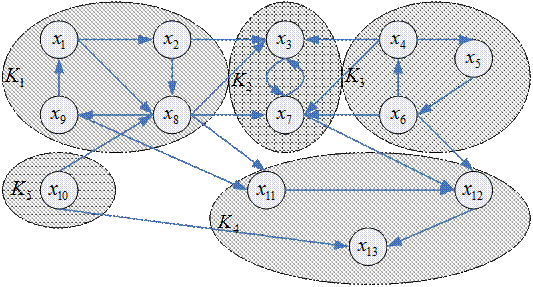
Пример
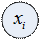- группировка, 
- отношение влияния.
Кланы – совокупности группировок с равными «правами» по отношению друг к другу и к внешним группировкам.
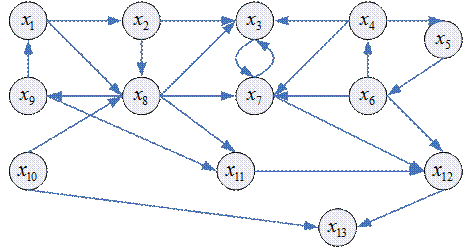
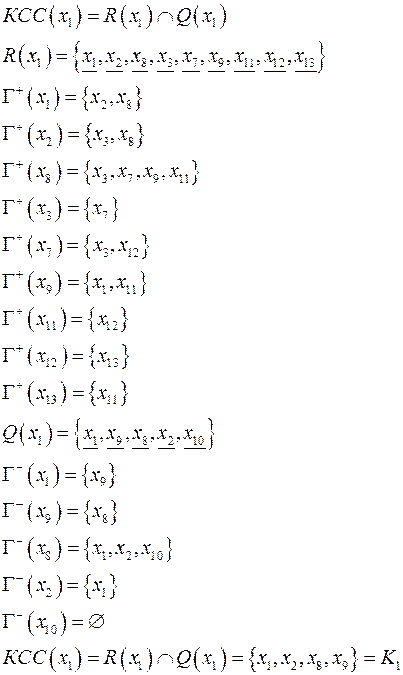
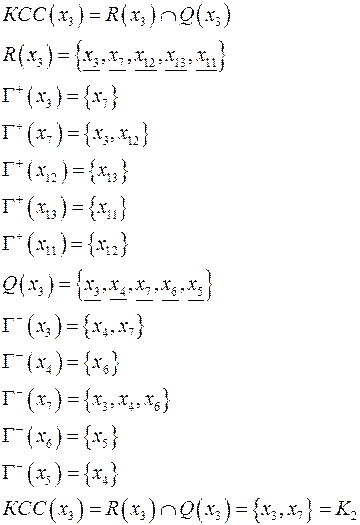
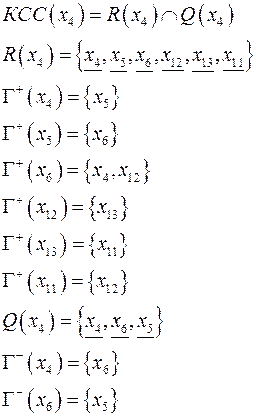
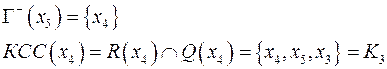
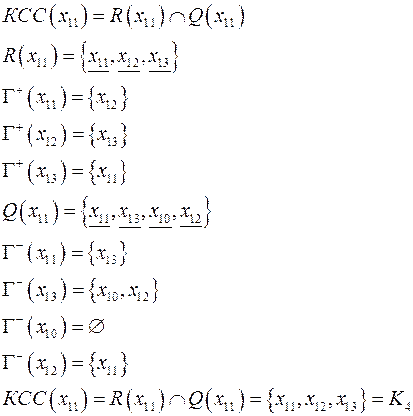
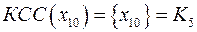
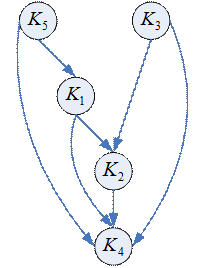
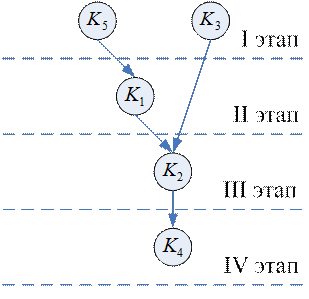
Орграф, в котором отсутствуют контуры, называется сетью. В сети есть следующие особые элементы:
вершина-исток ( )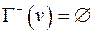 
| вершина-сток ( )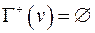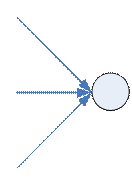 
|
Каждая вершина в сети является компонентой сильной связности. Пусть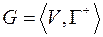 
- орграф и 
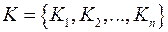- его КСС. Конденсатом орграфа 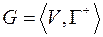называется сеть, которая получена из орграфа путем сжатия каждой КСС в одну вершину.
Цикл в графе называется Эйлеровым, если любое ребро графа участвует в его образовании ровно один раз. Граф, содержащий Эйлеров цикл называется Эйлеровым.
Теорема Эйлера
Граф является Эйлеровым тогда и только тогда, когда степени всех его вершин четные.
Цикл в графе называется Гамильтоновым, если каждая вершина графа участвует в его образовании ровно один раз. Граф, содержащий Гамильтонов цикл называется Гамильтоновым.
Свойства «Эйлеровости» и «Гамильтоновости» являются независимыми.
