Нахождение компонент связности
Компоненты связности графа
Максимальный по включению вершин подграф графа, любые две вершины которого связны (имеется ввиду вершины подграфа) называется компонентой связности графа.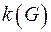 
- число компонент связности графа.
Теорема
Любая вершина графа принадлежит ровно одной компоненте связности.
Число компонент связности графа 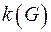является инвариантом. Если 
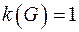, то граф связен. Инварианты 
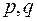и 
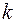являются зависимыми друг от друга.
Теорема
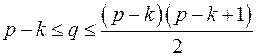
Следствие
Если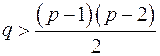 
, то граф связен (
).
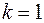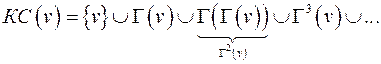
Шаг 0: поместить 
в список.
Итерационный шаг:
1. Найти в списке первую непросмотренную вершину (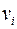
).
2. Вычислить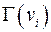 
и добавить в список те вершины из окрестности, которых нет в списке.
3. Отметить 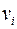как просмотренную.
Заключительный шаг: Итерационный шаг выполняется до тех пор пока в списке есть непросмотренные вершины.
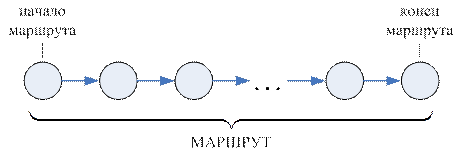
Если начальная вершина совпадает с конечной, то такой маршрут называется контуром. Две вершины 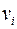и 
сильно связны, если существует маршрут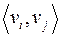 
и существует маршрут 
.
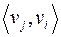Орграф называется сильно связным, если любые две его вершины сильно связны.
Пример
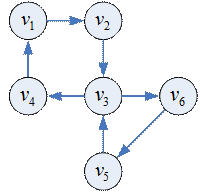
Максимальный по включению вершин подграф орграфа, любые две вершины которого сильно связны, называется компонентой сильной связности орграфа (КСС).
Отношение сильной связности является отношением эквивалентности на множестве вершин. Таким образом разбиение орграфа на КСС – это разбиение множества вершин на классы эквивалентности.
