Длина вектора
Координаты вектора
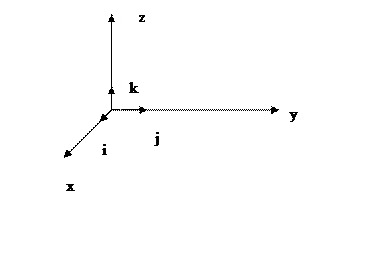
Декартова система координат.
Свойства
1. 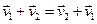 ;
;
2. 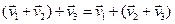 ;
;
3. существует нулевой вектор 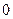 такой, что
такой, что 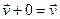 ;
;
4. существует противоположный элемент  такой, что
такой, что  ;
;
Для любых 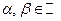 и любых
и любых 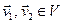
5. 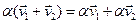 ;
;
6. 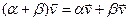 ;
;
7. 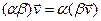 ;
;
8. 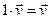 .
.
определениеДекартовым базисом в пространстве называются 3 попарно ортогональных, имеющих единичную длину вектора 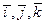 исходящих из общего начала т.О.
исходящих из общего начала т.О.
определениеДекартова система координат в пространстве это 3 прямые проходящие через общее начало т. О, содержащие векторы декартова базиса 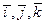 и имеющие такое же направление.
и имеющие такое же направление.
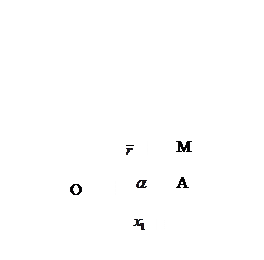
В пространстве возьмем т. 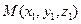 , проведем радиус-вектор этой точки.
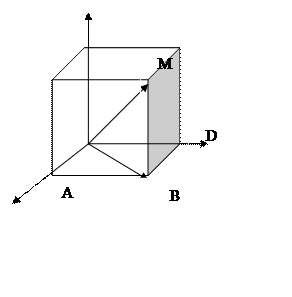
, проведем радиус-вектор этой точки.  . Через т.М проведем проецирующие плоскости, перпендикулярно осям координат, получим прямоугольный параллелепипед.
. Через т.М проведем проецирующие плоскости, перпендикулярно осям координат, получим прямоугольный параллелепипед.
 Это разложение вектора r по базису
Это разложение вектора r по базису 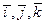 . Коэффициенты разложения — это координаты вектора.
. Коэффициенты разложения — это координаты вектора.  .
.
Вектор 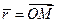 является диагональю прямоугольного параллелепипеда.
является диагональю прямоугольного параллелепипеда.  — ребра. Квадрат диагонали = сумме квадратов его ребер.
— ребра. Квадрат диагонали = сумме квадратов его ребер.
 .
.






 Из
Из 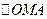

Возводим в квадрат и складываем. 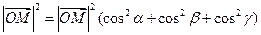
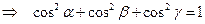 .
.
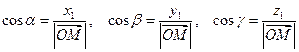 .
.