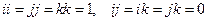Проекция вектора.
Критерий коллинеарности векторов в координатной форме.
Линейные операции над векторами в координатной форме.
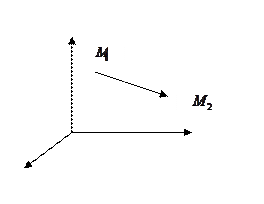
Координаты вектора через координаты начала и конца вектора.
Единичный вектор направления.
Пусть дан вектор 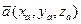 . Тогда вектор
. Тогда вектор 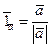 имеет координаты
имеет координаты 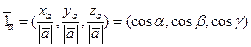
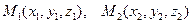
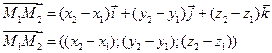
Пусть даны два вектора
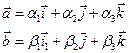
1) Сложение
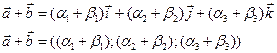
2) Умножение на число
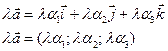
Пусть даны два вектора
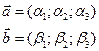
Они коллениарны, если 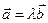
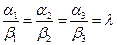
При  , то
, то 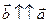 ; если
; если 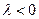 , то
, то 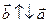 .
.
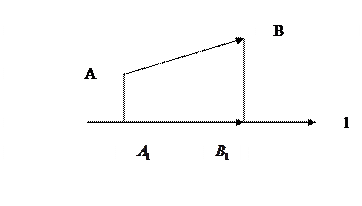
Пусть дана ось l и вектор АВ. Спроецируем т. А и т.В на ось.
определениеГеометрической проекцией вектора АВ на ось l называется вектор 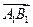 .
.
определениеЧисловой проекцией (или просто проекцией) называется число равное длине его геометрической проекции, взятой со знаком + если АВ и l сонаправлены.
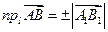
1. Свойства проекций.
2. Проекция суммы равна сумме проекций
3. Равные векторы имеют равные проекции
4. При умножении вектора на число, проекция умножается на это число
5. 
определениеСкалярное произведение векторов 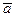 и
и 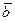 называется число равное произведению длин этих векторов на косинус угла между ними.
называется число равное произведению длин этих векторов на косинус угла между ними.
Обозначения: 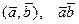
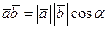
Свойства
1. 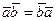
2. 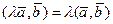
3. 
4. 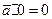
Утверждения
1. Если 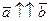 , то
, то 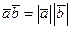
2. Если 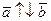 , то
, то 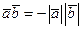
3. Если 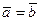 , то
, то 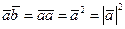 ,
, 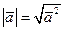
4. 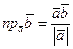
5. 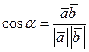
6. Условие ортогональности 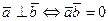 .
.
7.