Конечная форма радикального признака Коши.
Радикальный признак Коши.
Пусть 
, тогда ряд 
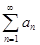сходится.
Пусть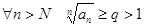 
, тогда ряд 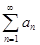расходится.
Доказательство. Пусть . Тогда 
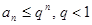, ряд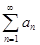сходится по первому признаку сравнения с бесконечно убывающей геометрической прогрессией.
Пусть 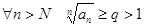. Тогда 
, ряд 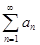расходится, так как необходимый признак сходимости ряда не выполнен.
Пусть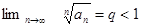 
, тогда ряд 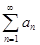сходится.
Пусть 
, тогда ряд 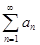расходится.
Доказательство. Пусть 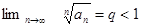, тогда 
.
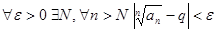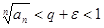при малом 
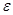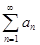. Ряд сходится по конечной форме радикального признака Коши.
Пусть , тогда .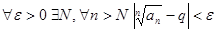 
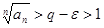при малом 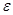. Тогда , ряд 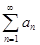расходится, так как необходимый признак сходимости ряда не выполнен.
Пример.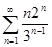 
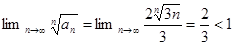, ряд сходится по радикальному признаку Коши в предельной форме.
Замечание. У каждого признака сходимости есть своя «зона нечувствительности». Ни признак Даламбера, ни радикальный признак Коши не позволяют установить расходимость гармонического ряда. Проверьте это. Гармонический ряд расходится, но расходится так слабо, что попадает в «зону нечувствительности» указанных признаков. Интегральный признак Коши имеет меньшую «зону нечувствительности» и позволяет установить расходимость гармонического ряда.
