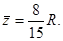Приложения тройного интеграла.
Сферическая система координат.
Цилиндрическая система координат.
  
| Вводятся цилиндрические координаты r, j, h.
x = r cosj, y = r sinj, z = h. Вычислим якобиан
|
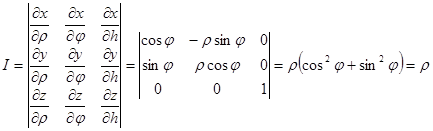
Пример Вычислить объем пространственного тела, заключенного между цилиндрической поверхностью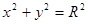 
и эллиптическим параболоидом 
.
.
=
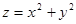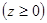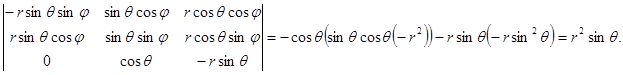
Пример. Найти массу части шара (с центром в начале координат, радиусом R), находящейся в первом октанте, если плотность вещества шара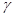 
в каждой точке шара пропорциональна расстоянию этой точки от оси OZ.
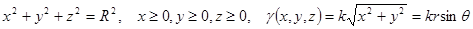
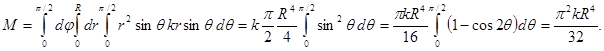
Геометрическое приложение – вычисление объема любого пространственного тела.
По свойству 3 тройного интеграла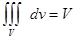 
, где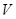 
– объем области V.
С помощью двойного интеграла тоже можно вычислять объем, но только цилиндрического тела, а не произвольного.
Пример. Вычислить объем пространственного тела, ограниченного эллиптическим параболоидом 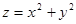и шаром ( единичного радиуса с центром в точке (0, 0, 1))
.
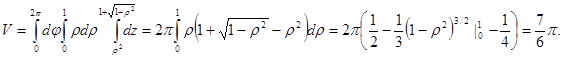
Механические приложения – вычисление массы пространственного тела, статических моментов, центра тяжести, моментов инерциипо формулам, которые выводятся аналогично соответствующим формулам для плоского тела с двойным интегралом (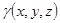
- плотность вещества тела в каждой точке).
, 
, 
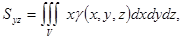
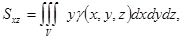
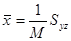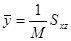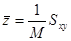. Формулы для моментов инерции запишите сами (например, 
)
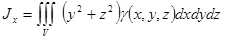Пример. Определить координаты центра тяжести полушара 
, 
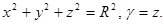По симметрии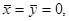 
. 
, 
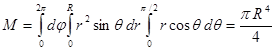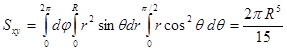