Краевая задача Римана
Дополнение к теореме о вычетах
Если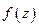 
имеет конечное число особых точек, то в 
:
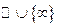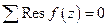
Доказательство: 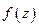имеет конечное число конечных особых точек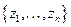 
: 
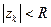
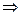(по 1-й Теореме о вычетах)
+
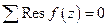, ч.т.д.
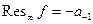, где 
- коэффициент при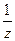 
при разложении 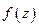в ряд Лорана в окрестности 
.
Замечание.
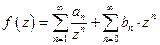
В окрестности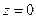 
: 
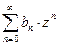- правильная часть ряда Лорана
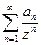- главная часть ряда Лорана
В окрестности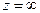 
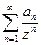: - правильная часть ряда Лорана
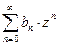- главная часть ряда Лорана
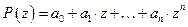- в 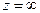полюс.
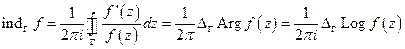
То же самое понятие индекса применяется для функции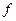 
по кривой 
.
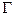Пусть 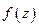аналитична вне кривой 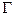, тогда
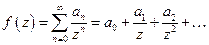
Пусть число нулей с учетом кратностей 
, тогда
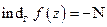
Если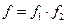 
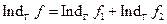
Формулировка задачи Римана:
Пусть ,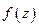 
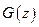- функция на 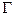(замкнутая).
Требуется найти две аналитических функции
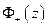внутри ,
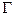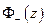вне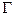
так, чтобы выполнялось:
o Для предельных значений на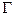
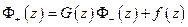
o Однородная задача Римана (
)
I шаг.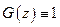 
, 
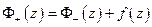
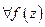(непрерывность по Гёльдеру)
Рассмотрим интеграл Коши
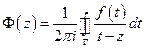
По формулам Сохоцкого
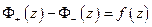
II шаг. Пусть имеем решение однородной задачи
Найдем индексы от обеих частей равенства
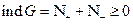
1.) 
, предположим, что 
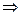
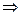функция 
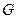однозначна, существует 
.
Решим задачу
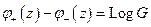
По формулам Сохоцкого
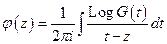
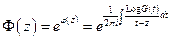
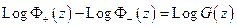
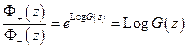
2.) 
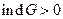(- неоднозначная функция)
Обозначим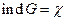 
, тогда
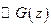
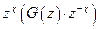
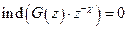
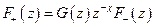
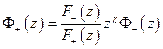
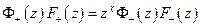
- аналитична внутри, 
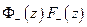- аналитична вне
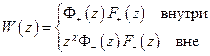
аналитична во всей плоскости 
, на у неё полюс порядка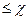 
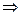
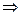
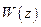- полином.
