Формула Пуассона
Задача Дирихле
Пусть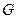 
- область, 
.
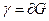На границе задана функция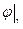 
.
Требуется найти гармоническую функцию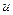 
: 
в .
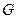Для граничных значений имеем 
.
Утв. Для ограниченной области 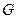задача Дирихле имеет единственное решение.
Единственность: Пусть 
, 
- два решения
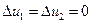
в точке 
, то минимум (максимум) достигается внутри области.
Принцип экстремума 
Существование: 
- единичный круг.
Решение можно получить по формуле Пуассона.
Предположим, что задача Дирихле имеет решение,
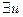, в 
, 
.
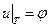Найдем сопряженную гармоническую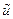 
.
- аналитична в .
Напишем формулу Коши:
, 
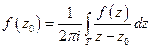Возьмем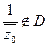 
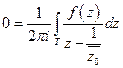
Вычтем
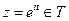
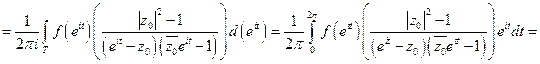
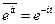
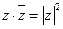
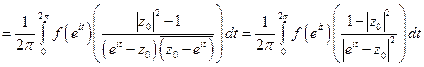
Разбиваем на вещественную и мнимую части
