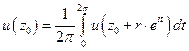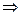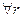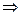Теорема о среднем для гармонических функций
Гармонические функции
- гармоническая, если 
в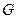 
.
Если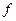 
- аналитическая 
, то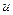 
, 
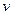- гармонические
; 
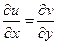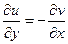
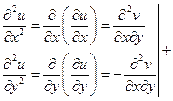
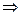
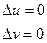
Справедливо обратное, если 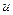- гармоническая, то существует гармоническая 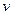(которая называется сопряженной гармонической) так, что 
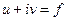- аналитическая 
, 
.
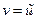Доказательство: 
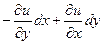является полным дифференциалом некоторой функции .
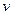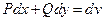
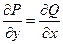
верно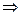
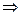
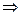
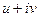- аналитическая
Функция 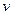находится интегрированием
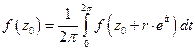
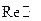
Гармоническая функция достигает минимума или максимума только на границе области.
- точка максимума
