Теорема Коши.

Пусть 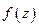аналитична в 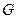, , 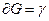тогда:

1)

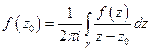
2)

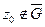
Доказательство:

2) 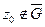, функция - аналитическая в

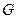
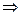
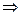по Формуле Коши .

1) Построим окружность ,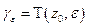

- аналитична в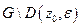

Формула Коши .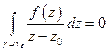

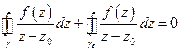
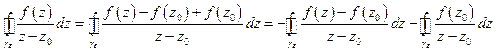
II интеграл вычисляется в явном виде

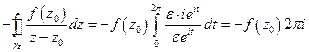
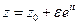- точка окружности

I интеграл есть 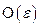, проверяем

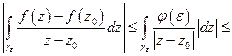
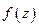(аналитична, следовательно непрерывна, поэтому )

.

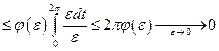
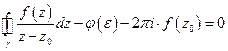
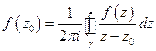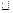
Следствие 1. (Теорема о среднем)

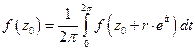для аналитических функций.

Доказательство: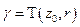

Следствие 2. (Принцип max модуля)

Если 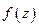аналитична в 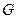, 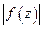достигает максимума во внутренней точке области 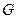, то .